Правило сложения дисперсий

Наряду с изучением вариации признака по всей совокупности в целом бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии. Выделяют три вида дисперсии: общую, внутригрупповую и межгрупповую.

Общая дисперсия (σ²) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию,'

.

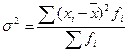Внутригрупповая дисперсия ( 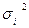) отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она вычисляется следующим образом:

,

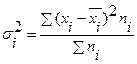где n_i— число единиц в каждой выделенной группе;

— среднее значение признака в i-й группе.

Средняя из внутригрупповых дисперсий ( ) равна

Межгрупповая дисперсия (δ_x²) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле

Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий

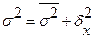
Данное соотношение называется правилом сложения дисперсий.

Оно используется в ряде методов статистики, в частности при расчете ошибок выборочного наблюдения и при измерении тесноты связи между признаками (см. далее). Теоретический и практический интерес этого правила заключается, во-первых, в том что, зная две величины, мы на основе приведенного равенства всегда можем определить третью величину. Второе важное значение этого правила состоит в том что, зная общую дисперсию и дисперсию групповых средних, мы имеем право (если группировка произведена правильно) судить о силе влияния группировочного признака с помощью эмпирического коэффициента детерминации и эмпирического корреляционного отношения.

Эмпирический коэффициент детерминации (η²) представляет собой долю межгрупповой дисперсии в общей дисперсии и рассчитывается по формуле

.

Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленного вариацией группировочного признака.

Эмпирическое корреляционное отношение (η) представляет собой корень квадратный из эмпирического коэффициента детерминации и рассчитывается следующим образом:

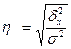(6.5)

Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если η = 0, то признак не оказывает влияние на результативный. Если η = 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.

Пример.

Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую и общую дисперсии по данным табл. 6.3, характеризующим производительность труда двух бригад рабочих.

Таблица 6.3

1-я бригада	2-я бригада
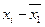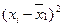
№ рабочего	Изготовлено деталей за час, шт., хi	( )		№ рабочего	Изготовлено деталей за час, шт., х.	( )
		-2				-3
		-1				-2
						+1
						-1
						+3
						+2
Итого		-		Итого		-

Решение.

Для расчета групповых дисперсий вычислим средние по каждой группе (графы 2 и 6):

Промежуточные расчеты дисперсий по группам представлены в табл. 6.3, графы 3,4,7 и 8. Подставив полученные значения в формулу, получим

,

.

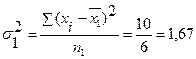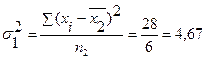Средняя из групповых дисперсий равна

Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:

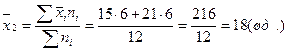
Теперь определим межгрупповую дисперсию

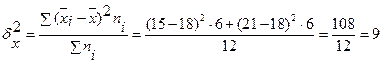
Таким образом, общая дисперсия по правилу сложения дисперсий равна

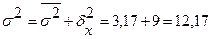
На основании правила сложения дисперсий определим эмпирическое корреляционное отношение по формуле (6.5)

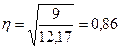
Величина 0,86 характеризует существенную связь между группировочным и результативным признаками.

Разделы «Моменты распределения», «Изучение формы распределения», «Критерии согласия», «Вариационный ряд и группировка» отводятся на самостоятельное изучение.