Средняя гармоническая и средняя геометрическая

Кроме средней арифметической при расчете статистических показателей могут использоваться и другие виды средних. При этом следует учитывать, что в каждом конкретном случае, в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель.

Формула средней гармонической взвешенной

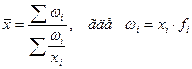
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса 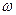за ряд временных интервалов.

Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:

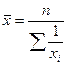
Средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения 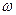, для единиц совокупности равны.

Следует отметить, что средняя гармоническая взвешенная, как и средняя арифметическая взвешенная, в расчетах используются значительно чаще аналогичных невзвешенных формул. Это объясняется тем, что на практике достаточно редко имеют место ситуации, когда веса осредняемых вариантов равны (одинаковое отработанное время, одинаковая численность работников в группах, одинаковый товарооборот торговых предприятий и т. п.).

Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая

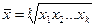— невзвешенная; 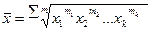- взвешенная.

Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе.

Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:

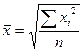-невзвешенная; 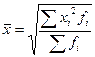-взвешенная.

Наиболее широко этот вид средней используется при расчете показателей вариации, коэффициентов структурных сдвигов, индексов.

В статистическом анализе также применяются степенные средние 3-го порядка и более высоких порядков.