Средняя арифметическая
Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной. Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.
Предположим, шесть торговых предприятий фирмы имеют следующий объем товарооборота за месяц:
| Торговое предприятие | ||||||
| Товарооборот (млн. руб.) |
Для того, чтобы определить средний месячный товарооборот в расчете на одно предприятие, необходимо воспользоваться следующим исходным соотношением:
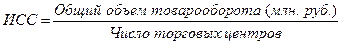
Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней
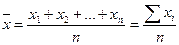
С учетом имеющихся данных получим
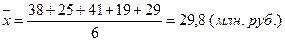
В данном случае мы использовали формулу средней арифметической простой (невзвешенной).
Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
 | |||
 |
Рассмотрим следующий условный пример:
Таблица 5.3 Сделки по акциям эмитента «X» за торговую сессию
| Сделка | Количество проданных акций, шт. | Курс продажи, руб. |
Определим по данному дискретному вариационному ряду средний курс продажи одной акции, что можно сделать только используя следующее исходное соотношение:
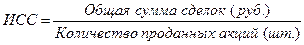
Чтобы получить общую сумму сделок необходимо по каждой сделке курс продажи умножить на количество проданных акций и полученные произведения сложить. В конечном итоге мы будем иметь следующий результат:
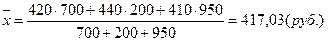
Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной
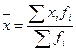 (1)
(1)
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Так, в приведенном выше примере количество проданных в ходе каждой сделки акций соответственно составляет 37,8% (0,378); 10,8% (0,108) и 51,4% (0,514) от их общего числа. Тогда, с учетом несложного преобразования формулы (1) получим
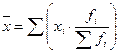
или
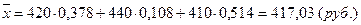
На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса в действительности необходимы. Предположим имеются следующие данные.
Таблица 4. Себестоимость единицы продукции «Z»
| Предприятия | Себестоимость единицы продукции, руб. |
Можно ли по имеющимся данным определить среднюю себестоимость данной продукции по двум предприятиям, вместе взятым? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. (доказательство этого правила будет приведено ниже). Однако на первом предприятии за рассматриваемый период может быть произведено, к примеру, 50 единиц продукции, а на втором — 700 единиц. Тогда для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная
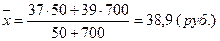
Общий вывод заключается в следующем: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Рассмотрим следующий пример.
Таблица 5.5.
Распределение сотрудников предприятия по возрасту
| Возраст (лет) | Число сотрудников (чел.) |
| до 25 | |
| 25-30 | |
| 30-40 | |
| 40-50 | |
| 50-60 | |
| 60 и более | |
| Итого |
Для определения среднего возраста персонала найдем середины возрастных интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). С учетом этого середины интервалов будут следующими:
22,5 27,5 35,0 45,0 55,0 65,0.

 Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия
Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия
_ 22,5·8 + 27,5·32 +35·68+ 45·49+ 55·21+ 65·3
х = _____________________________________= 38,6 (года).
8 + 32+68+49 + 21 + 3
Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства.
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
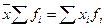
Действительно, если мы обратимся к приведенному выше примеру расчета среднего курса продажи акций (табл. 5.3), то получим следующее равенство (за счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться):
417,03 · 1850=420 · 700 + 440 ·200 + 410 ·950.
2. Сумма отклонений индивидуальных значений признака от
средней арифметической равна нулю
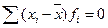 (5.2)
(5.2)
Для нашего примера:
(420 - 417,03) • 700 + (440 - 417,03) • 200 + (410 - 417,03) • 950 = 0.
Математическое доказательство данного свойства сводится к следующему:
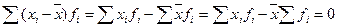
3. Сумма квадратов отклонений индивидуальных значений при
знака от средней арифметической меньше, чем сумма квадратов их
отклонений от любой другой произвольной величины С,
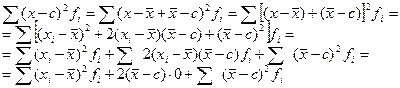
Следовательно, сумма квадратов отклонений индивидуальных шачений признака от произвольной величины С больше суммы кпадратов их отклонений от своей средней на величину
 или
или 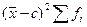
4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину
5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз
6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится
Исходя из данного свойства, можно заключить, что если все веса равны между собой, то расчеты по средней арифметической взвешенной и средней арифметической невзвешенной приведут к одному и тому же результату.
Дата добавления: 2015-10-13; просмотров: 1582;
