Структурные средние
Наиболее часто используемыми в экономической практике структурными характеристиками являются мода и медиана. Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Основное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
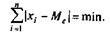
Определим моду и медиану по несгруппированным данным. Предположим, что 7 сотрудников отдела имеют следующий стаж работы (лет):
5 2 4 3 4 2 2.
Так как чаще всего встречается стаж 2 года, то он и будет модальным.
Для определения медианы необходимо провести ранжирование:
2 2-23445.
Центральным в этом ряду является стаж 3 года, следовательно, данный стаж и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.
Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной совокупности. В этих случаях средняя не позволяет объективно оценить исследуемую совокупность вследствие сильного влияния аномальных максимальных или минимальных значений.
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
Предположим., распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид:
| Цена, руб. | Число торговых предприятий |
| 21Q | |
| Итого |
Определение моды по дискретному вариационному ряду не составляет большого труда — наибольшую частоту (35 предприятий) имеет цена 214 руб., следовательно, она и является модальной.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:
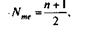
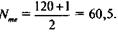
|
где n — объем совокупности.
В нашем случае
Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 60-м и 61-м предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 3 торговых предприятия, их также нет ни во второй группе (3 + 18 = 21), ни в третьей группе (3.+ 18 + 25 = 46). Следовательно, 60-е и 61-е предприятия находятся в четвертой группе (3 + 18 + 25 + 31 = 77), а значит, медианой является цена 213 руб.
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
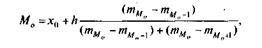
где х0 — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); h — ширина модального интервала; 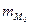 — частота модального интервала;
— частота модального интервала; 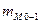 — частота интервала, предшествующего модальному;
— частота интервала, предшествующего модальному; 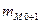 — частота интервала, следующего за модальным; и
— частота интервала, следующего за модальным; и
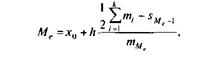
Где х0 — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); h — ширина медианного интервала: 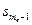 — накопленная частота интервала, предшествующего медианному; mi — частота i-го интервала, i = 1, 2,..., К;
— накопленная частота интервала, предшествующего медианному; mi — частота i-го интервала, i = 1, 2,..., К; 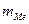 — частота медианного интервала.
— частота медианного интервала.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если М0< Ме< х — имеет место правосторонняя асимметрия, при х < Ме< Ма следует сделать вывод о левосторонней асимметрии ряда.
Дата добавления: 2015-10-13; просмотров: 645;
