Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
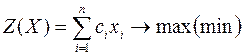
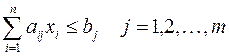
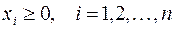
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
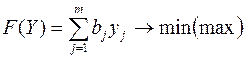
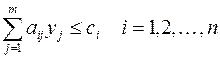
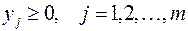
Переменные двойственной задачи 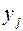 называют объективно обусловленными оценками или двойственными оценками.
называют объективно обусловленными оценками или двойственными оценками.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
1.целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид 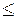 , а в задаче на минимум – вид
, а в задаче на минимум – вид 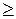 ;
;
2.матрица 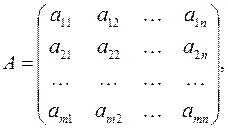 составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица
составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица 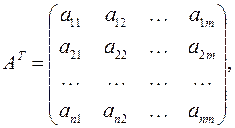 в двойственной задаче получаются друг из друга транспонированием;
в двойственной задаче получаются друг из друга транспонированием;
3.Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;
4.Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;
5.Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства 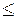 , соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
, соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.
| Исходная задача | Двойственная задача |
| Симметричные пары | |
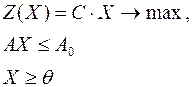
| 
|

| 
|
| Несимметричные пары | |

| 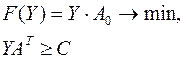
|

| 
|
где:
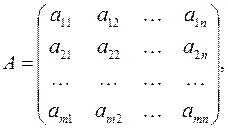
 ,
, 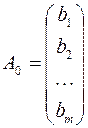 .
.
 ,
, 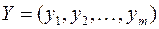
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья  и
и 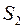 , остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров:
, остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров: 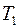 ,
,  и
и  .
.
| Виды товаров | 
| 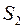
| Прибыль |
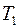
| |||

| |||

| |||
| Запасы |
При исследовании первой возможности (наладить выпуск товаров 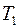 ,
,  и
и  ) возникает вопрос о плане выпуска, который задается тремя переменными
) возникает вопрос о плане выпуска, который задается тремя переменными 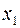 ,
, 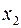 и
и  , которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:
, которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:

Прибыль, которую получит предприятие от реализации товара, составит:
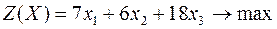
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи  и
и  будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже
будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже  и
и  предприятие будет терпеть убытки.
предприятие будет терпеть убытки.
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара  , то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
, то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
Это требование можно представить в виде системы неравенств:
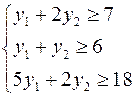
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара  , а в правой – прибыль от реализации этой единицы товара.
, а в правой – прибыль от реализации этой единицы товара.
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины 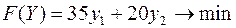 .
.
Дата добавления: 2015-10-09; просмотров: 1030;
