Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственности (теорема о дополняющей нежесткости):

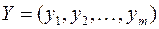Пусть – допустимое решение прямой задачи, а – допустимое решение двойственной задачи. Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

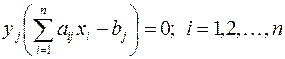
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.

Теорема об оценках:

Значения переменных 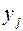в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов 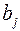системы ограничений – неравенств прямой задачи на величину :

.

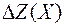Диапазон изменения компонент вектора , в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.

Экономический смысл первой теоремы двойственности следующий. План производства 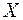и набор ресурсов 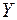оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции , равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов 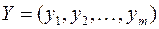. Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов , т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина 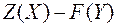характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.

Контрольные вопросы к лекции 14

1. Понятие математического моделирования.

2. Задача линейного программирования и ее каноническая форма.

3. Целевая функция и система ограничений.

4. Понятие выпуклой линейной комбинации.

5. Базисное, опорное и оптимальное решения.

6. Двойственная задача линейного программирования и объективно обусловленные оценки.

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ

1.Основы математической логики. Высказывания и логические связки.

2.Элементы теории множеств.

3.Основные операции над множествами.

4.Отображения.

5.Отношения эквивалентности и упорядоченности.

6.Числовые множества. Основные понятия.

7.Соединения. Бином Ньютона.

8.Комплексные числа. Операции над комплексными числами.

9.Формула Муавра. Извлечение корня из комплексного числа.

10.Векторы. Линейные операции над векторами. Проекция вектора на ось.

11.Линейная зависимость векторов. Базис. Координаты вектора в базисе.

12.Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении.

13.Направляющие косинусы. Скалярное произведение.

14.Векторное произведение. Смешанное произведение.

15.Прямая. Уравнения прямой.

16.Взаимное расположение прямых.

17.Плоскость. Нормальное уравнение плоскости.

18.Плоскость. Взаимное расположение плоскостей.

19.Кривые второго порядка. Эллипс.

20.Кривые второго порядка. Гипербола.

21.Кривые второго порядка. Парабола.

22.Исследование на плоскости уравнения второй степени.

23.Понятие евклидова пространства. 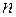– мерные векторы. Коллинеарные векторы.

24.Размерность и базис векторного пространства.

25.Матрицы. Основные понятия. Операции над матрицами.

26.Матрицы. Определитель матрицы. Обратная матрица. Ранг матрицы.

27.Понятие линейного оператора. Переход к новому базису. Линейное преобразование переменных.

28.Собственные значения и собственные вектора матриц.

29.Многочлены. Теорема о делении с остатком.

30.Многочлены. Теорема Безу.

31.Квадратичные формы.

32.Канонический базис квадратичной формы. Канонический базис из собственных векторов матрицы квадратичной формы. Канонический базис Якоби.

33.Положительно и отрицательно определенные квадратичные формы.

34.Применение квадратичных форм к исследованию кривых второго прядка.

35.Системы линейных уравнений. Критерий совместности системы линейных уравнений.

36.Системы линейных уравнений. Правило Крамера решения систем линейных уравнений. Метод Гаусса.

37.Однородные системы уравнений. Разрешенные системы линейных уравнений.

38.Задача линейного программирования. Приведение общей задачи линейного программирования к канонической форме.

39.Множества допустимых решений. Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками.

40.Теория двойственности. Теоремы двойственности. Двойственная задача линейного программирования.

ЛИТЕРАТУРА

1.Гринберг А.С., Плющ О.Б. и др. Высшая математика. Учебное пособие. Ч. I. Минск, АУ, 2002.

2.Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. II. Минск, АУ, 1994.

3.Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. I. Минск, АУ, 1994.

4.Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. V. Минск, АУ, 1996.

5.Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. VII. Минск, АУ, 2001.

6.Гринберг А.С., Белаш Т.В., Рухленко Е.В. и др. Математика для менеджера. Учебное пособие. Ч. III. Минск, АУ, 1996.

7.Гринберг А.С., Иванюкович В.А., Скуратович Е.А. Математика на персональном компьютере. Ч.VIII. Минск АУ. 2001.

8.Кастрица О.А. Высшая математика: примеры, задачи, упражнения. Учебное пособие для ВУЗов. Москва, ЮНИТИ, 2002.

9.Общий курс высшей математики для экономистов: Учебник/Под ред. В.И.Ермакова.– М.: ИНФРА-М, 2001. – 656 с.

10.Малыхин В.И. “Математика в экономике.” - М.: ИНФРА-М, 2002. – 352 с.

11.Кудрявцев В.А., Демидович Б.П. “Краткий курс высшей математики”. – М.: «Наука», 1975.

12.Кремер Н.Ш. и др. Высшая математика для экономистов. Москва, ЮНИТИ, 2001.

13.Колесников А.Н. "Краткий курс математики для экономистов". – М.: ИНФРА-М, 2001. – 208 с.

14.Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.: МГУ, Издательство «ДИС», 1997. – 368 с.

15.Жевняк Р.М., Карпук А.А. Высшая математика. Минск, Высшая школа, 1992.

16.Кузнецов А.В. и др. Высшая математика: Общий курс. Минск, Высшая школа, 1993.

17.Гусак А.А., Гусак Г.М. Справочник по высшей математике. Минск, Навука и тэхнiка, 1991.

18.Крынский Х.Э. Математика для экономистов. Москва, Статистика, 1970.

19.В.Т.Воднев и др. Математический словарь высшей школы. Мн., Высшая школа, 1984.

Учебное издание

Плющ Олег Борисович