Если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
Если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 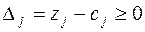 , то полученный план является оптимальным.
, то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор 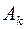 ,давший минимальную отрицательную величину симплекс-разности:
,давший минимальную отрицательную величину симплекс-разности: 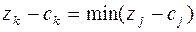 .
.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 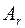 г, который дает минимальное положительное отношение:
г, который дает минимальное положительное отношение:
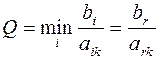 ;
; 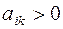 ,
, 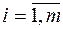 .
.
Строка 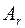 называется направляющей, столбец
называется направляющей, столбец 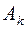 и элемент
и элемент
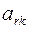 — направляющими(последний называют также разрешающимэлементом).
— направляющими(последний называют также разрешающимэлементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
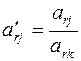 ,
, 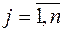
а элементы любой другой 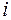 -й строки пересчитываются по формулам:
-й строки пересчитываются по формулам:
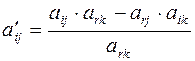 ,
, 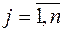 ,
, 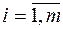
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
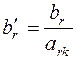 для
для 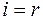 ;
; 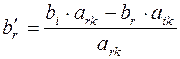 ,
, 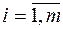 для
для 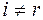 .
.
Если наименьшее значение 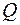 достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение 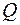 на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс-метода к минимизации линейной формы 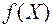 следует искать максимум функции
следует искать максимум функции 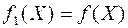 , затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
, затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки 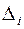 теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М–задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М–задачи содержит искусственные векторы или М–задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Дата добавления: 2015-10-09; просмотров: 907;
