Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью  . В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые т векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: 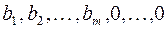 .
.
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
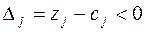 , где
, где 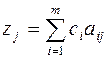 ,
, 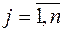
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
Дата добавления: 2015-10-09; просмотров: 975;
