Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

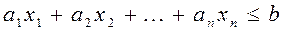
прибавляется величина 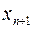, такая, что переводит неравенство в равенство 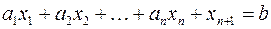, где:

.

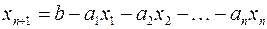Неотрицательная переменная 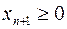называется дополнительнойпеременной.

Основания для возможности такого преобразования дает следующая теорема.