Взаимное расположение плоскостей

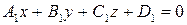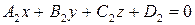Пусть даны плоскости и . Угол между ними равен углу между перпендикулярными к ним векторам 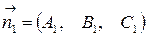и 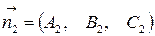. Косинус этого угла вычисляется по формуле:

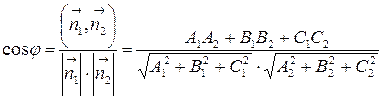
(6.5)

Плоскости параллельны, есл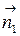и и коллинеарны, т.е.:

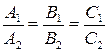
(6.6)

Условие перпендикулярности плоскостей ‑ 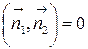, т.е.:

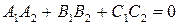
(6.7)

Если даны три плоскости:

,

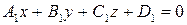
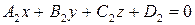
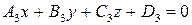(6.8)

то их общие точки определяются системой уравнений (6.8).

В случае, если перпендикулярные этим плоскостям векторы 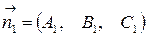, , 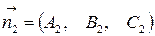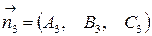некомпланарны, три плоскости имеют единственную общую точку.

В самом деле, тогда смешанное произведение 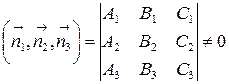, а записанный определитель является определителем системы уравнений (6.8), и, следовательно, система (6.8) имеет единственное решение.

Контрольные вопросы к лекции №6

1. Понятие поверхности 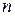-го порядка.

2. Общее уравнение плоскости.

3. Понятие нормального вектора плоскости.

4. Уравнение плоскости в отрезках.

5. Нормальное уравнение плоскости.

6. Вычисление отклонения точки от плоскости.