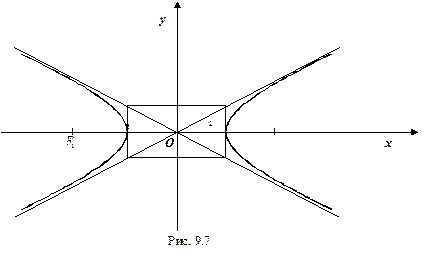Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 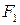 и
и 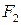 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 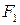 и
и 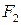 ).
).
Точки 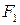 и
и 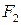 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 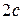 . Модуль расстояний от точек гиперболы до фокусов
. Модуль расстояний от точек гиперболы до фокусов 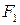 и
и 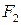 обозначим через
обозначим через 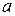 . По условию,
. По условию, 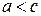 .
.
Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:
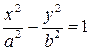
| (7.6) |
где 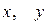 ‑ координаты произвольной точки гиперболы,
‑ координаты произвольной точки гиперболы, 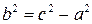 .
.
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 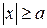 . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми
. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми 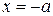 и
и 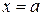 .
.
Так как в уравнение входят только четные степени 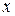 и
и 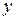 , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем: 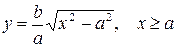 .
.
График этой функции от точки 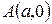 уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
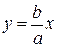
| (7.7) |
|

|


|
| |
|
|


Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты 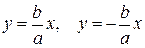 .
.
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 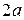 и
и 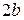 параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
|

Рис 7.8.
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 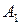 и
и 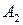 пересечения гиперболы с осью
пересечения гиперболы с осью 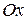 называются вершинами гиперболы. Величины
называются вершинами гиперболы. Величины 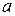 и
и 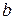 называются полуосями гиперболы. Если
называются полуосями гиперболы. Если 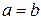 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Эксцентриситетом гиперболы называется число 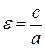 . Для любой гиперболы
. Для любой гиперболы 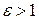 . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси
. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси 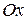 . На рисунке 7.9 изображены гиперболы с различными значениями
. На рисунке 7.9 изображены гиперболы с различными значениями 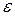 .
.
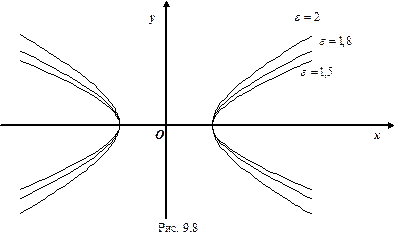
Рис. 7.9
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами 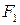 и
и 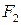 . Их длины
. Их длины 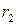 и
и 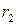 задаются формулами:
задаются формулами:
Для правой - ветви 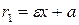 ,
,
Для левой - ветви 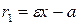 .
.
Прямые 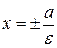 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением 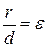 .
.
Дата добавления: 2015-10-09; просмотров: 1303;