Нормальное уравнение плоскости
Нормальным уравнением плоскости называется уравнение:
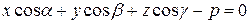 , ,
| (6.4) |
где 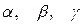 ‑ углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а
‑ углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а 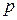 ‑ расстояние от плоскости до начала координат.
‑ расстояние от плоскости до начала координат.
Нормальное уравнение отличается от общего уравнения тем, что в нем коэффициенты при 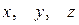 являются координатами единичного вектора
являются координатами единичного вектора 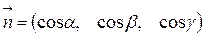 , перпендикулярного плоскости, а свободный член – отрицательный.
, перпендикулярного плоскости, а свободный член – отрицательный.
Общее уравнение (1) приводится к нормальному виду умножением его на нормирующий множитель 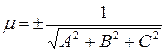 , при этом знак выбирается противоположным знаку свободного члена
, при этом знак выбирается противоположным знаку свободного члена 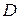 (если
(если 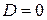 , знак можно выбрать любой).
, знак можно выбрать любой).

Отклонением 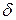 точки
точки 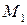 от плоскости называется ее расстояние
от плоскости называется ее расстояние 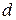 от плоскости, взятое со знаком плюс, если точка
от плоскости, взятое со знаком плюс, если точка 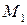 и начало координат
и начало координат 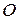 лежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус – если
лежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус – если 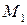 и
и 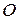 лежат по одну сторону от плоскости.
лежат по одну сторону от плоскости.
Отклонение точки 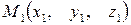 от плоскости определяется по формуле
от плоскости определяется по формуле 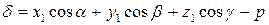 .
.
Следовательно, чтобы найти расстояние от точки до плоскости, надо привести уравнение плоскости к нормальному виду и в его левую часть вместо 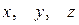 подставить координаты точки
подставить координаты точки 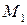 . Получим отклонение
. Получим отклонение 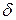 . А расстояние
. А расстояние 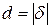 .
.
Дата добавления: 2015-10-09; просмотров: 842;
