Взаимное расположение прямых

Пусть даны две прямые:

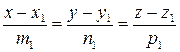и .

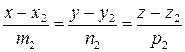Эти прямые заданы своими точкам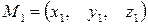и и 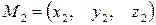и направляющими векторам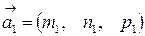и и 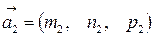. Поэтому:

.

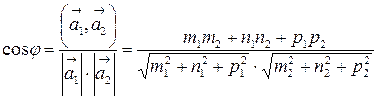Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямых можно записать в виде:

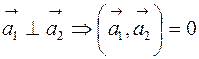или .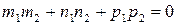

Условие параллельности: .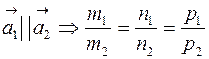

Возможны четыре случая взаимного расположения прямых:

I. Прямые совпадают: 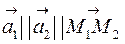, т.е.

.

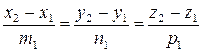II. Прямые параллельны: 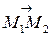непараллелен 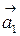, но 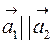, т.е. .

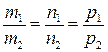III. Прямые пересекаются: 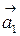непараллелен 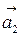, но 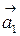, , 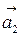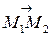‑ компланарны, т.е.

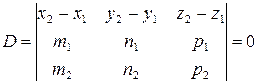
(5.8)

IV. Прямые скрещиваются: 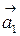, , 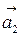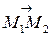‑ некомпланарны, т.е. .

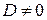Условие (5.8) выполняется в случаях I-III и означает, что прямые лежат в одной плоскости.

Контрольные вопросы к лекции №5

1. Общее уравнение прямой.

2. Понятие направляющего и нормального вектора прямой.

3. Каноническое уравнение прямой.

4. Векторное параметрическое уравнение прямой.

5. Уравнение прямой, проходящей через две точки.

6. Расчет угла между прямыми.

7. Условия пересечения, параллельности и перпендикулярности прямых.