Взаимное положение прямых

Прямые в пространстве могут быть параллельными, пересекающимися, скрещивающимися и перпендикулярными. Пространственные чертежи и эпюры параллельных и пересекающихся прямых представлены на рисунке 2.7а, б.

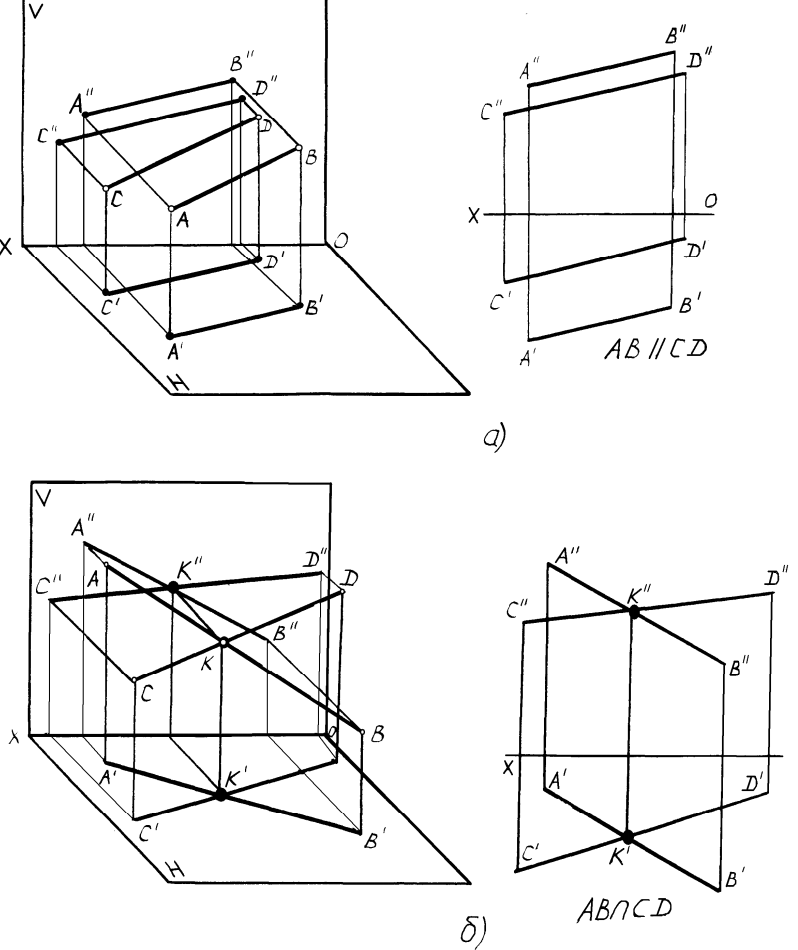
Рисунок2.7 – Параллельные и пересекающиеся прямые

Признаком параллельных прямых на эпюре является параллельность

их одноименных проекций.

Пересекающимися прямыми называются прямые, которые имеют

общую точку– точку пересечения. Признаком пересекающихся прямых на

эпюре является то, что проекции точки пересечения находятся на одной

линии связи.

Частным случаем пересекающихся прямых являются

перпендикулярные прямые. В соответствии с теоремой о проецировании

прямого угла, прямой угол будет проецироваться на плоскость проекций в

натуральную величину в том случае, когда одна из его сторон будет

параллельна этой плоскости проекций (Рисунок2.8).

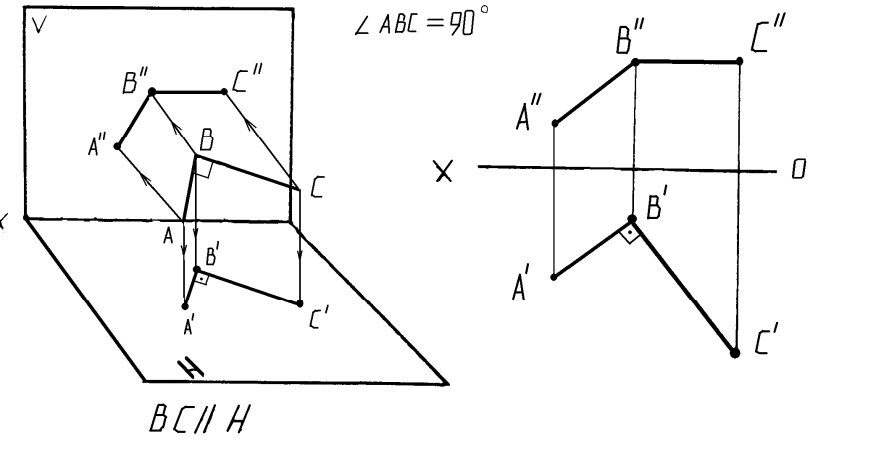
Рисунок2.8 – Перпендикулярные прямые

Скрещивающимися прямыми называются непараллельные прямые, не имеющие общей точки. Скрещивающиеся прямые в пространстве не пересекаются, но на эпюре их одноименные проекции накладываются друг на друга, что создает впечатление пересечения.

Признаком скрещивающихся прямых на проекциях является то, что проекции их мнимых точек пересечения не находятся на одной линии связи (рисунок 2.9а). В мнимых точках пересечения конкурируют две точки, принадлежащие разным прямым, или, другими словами, в мнимых точках конкурируют две прямые. Назовем эту область конкурирующим местом. При рассмотрении скрещивающихся прямых возникает вопрос о видимости проекций прямых в конкурирующих местах. Этот вопрос может быть решен методом конкурирующих точек (конкурирующих прямых).

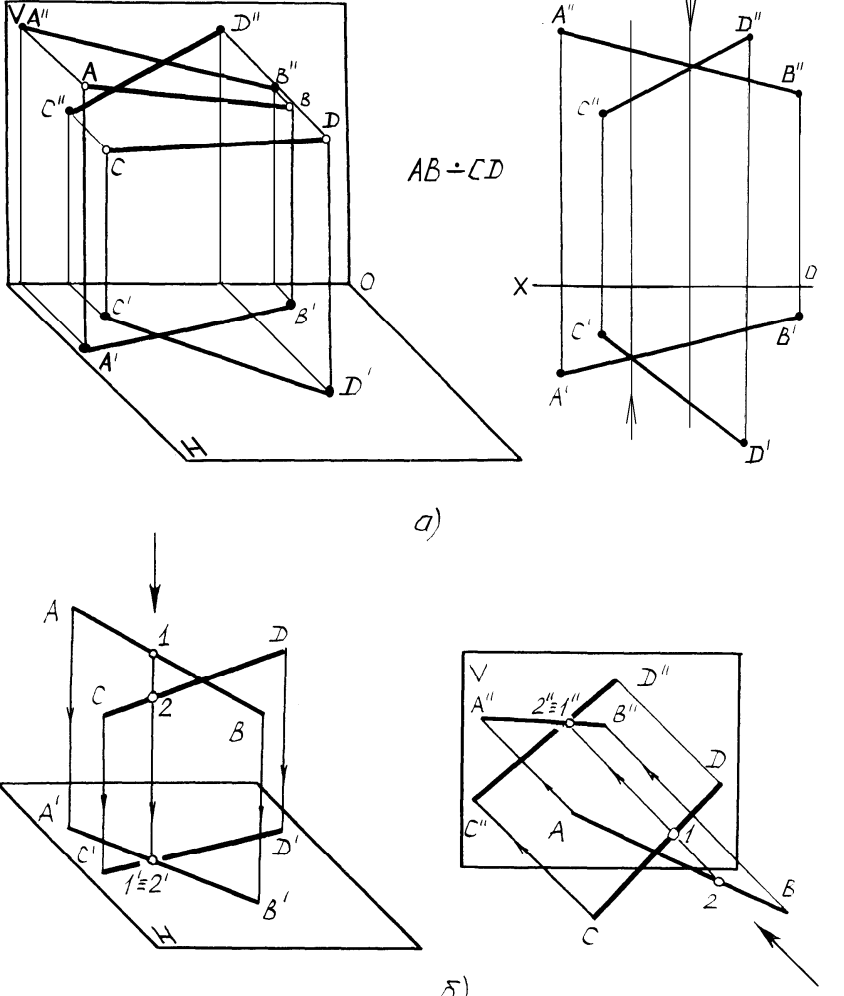
Рисунок2.9 – Скрещивающиеся прямые

Сущность метода заключается в следующем:

1) Отметить конкурирующее место на рассматриваемой проекции;

2) Обозначить конкурирующие точки или записать, какие прямые

конкурируют;

3) Провести через конкурирующее место линию связи;

4) Вдоль линии связи сравнить недостающие координаты

конкурирующих точек или конкурирующих прямых;

5) На рассматриваемой проекции будет видна та точка или прямая,

которая имеет наибольшую недостающую координату.

Так на рисунке 2.9б на горизонтальной проекции будет видна точка

1, принадлежащая прямой AB, или, проще говоря, прямая AB, так как

аппликата прямой AB вдоль линии связи наибольшая. На фронтальной

проекции также будет видна прямая AB, так как у неё в конкурирующем

месте наибольшая ордината.