Определение натуральной величины прямой

Так как прямая общего положения проецируется на плоскости проекций с искажением, то задача определения натуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямой разработан метод прямоугольного треугольника, сущность которого понятна из пространственного чертежа (рисунок 2.4а). Для того, чтобы определить натуральную величину прямой по её проекциям, необходимо на одной из её проекций (на любой) построить прямоугольный треугольник, одним катетом которого является сама проекция, а другим катетом– разность недостающих координат концов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 2.4б). Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например,горизонтальная проекция прямой строится по координатам X и Y её концов. Координата Z в построениях не участвует и называется недостающей координатой. Таким образом, при построении прямоугольного треугольника на горизонтальной проекции прямой на катете откладывают разность аппликат, а при построении на фронтальной проекции – разность ординат. При определении НВ прямой методом прямоугольного треугольника одновременно можно определить углы наклона прямой к плоскостям проекций (углы αο и βο). Они определятся как углы между гипотенузой и соответствующей проекцией прямой.

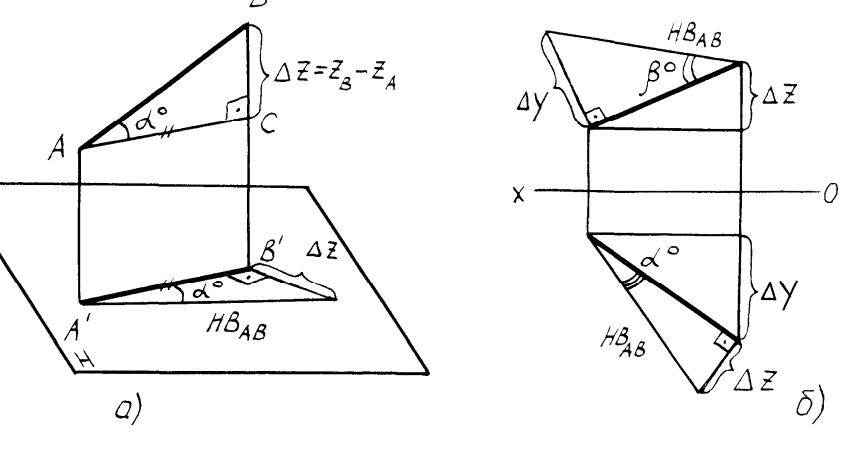
Рисунки 2.4 – Метод прямоугольного треугольника

Следы прямой

Точки пересечения прямой с плоскостями проекций называются следами прямой. В точках следов прямая переходит из одного октанта в другой. Различают горизонтальный, фронтальный и профильный следы прямой и их соответствующие проекции. На рисунке 2.5 показаны пространственные чертежи прямых общего и частного положения и образование их следов. Прямые, параллельные плоскостям проекций, имеют только два следа, а прямые, перпендикулярные плоскостям проекций, - один след, совпадающий с той проекцией прямой, на которой она проецируется в точку.

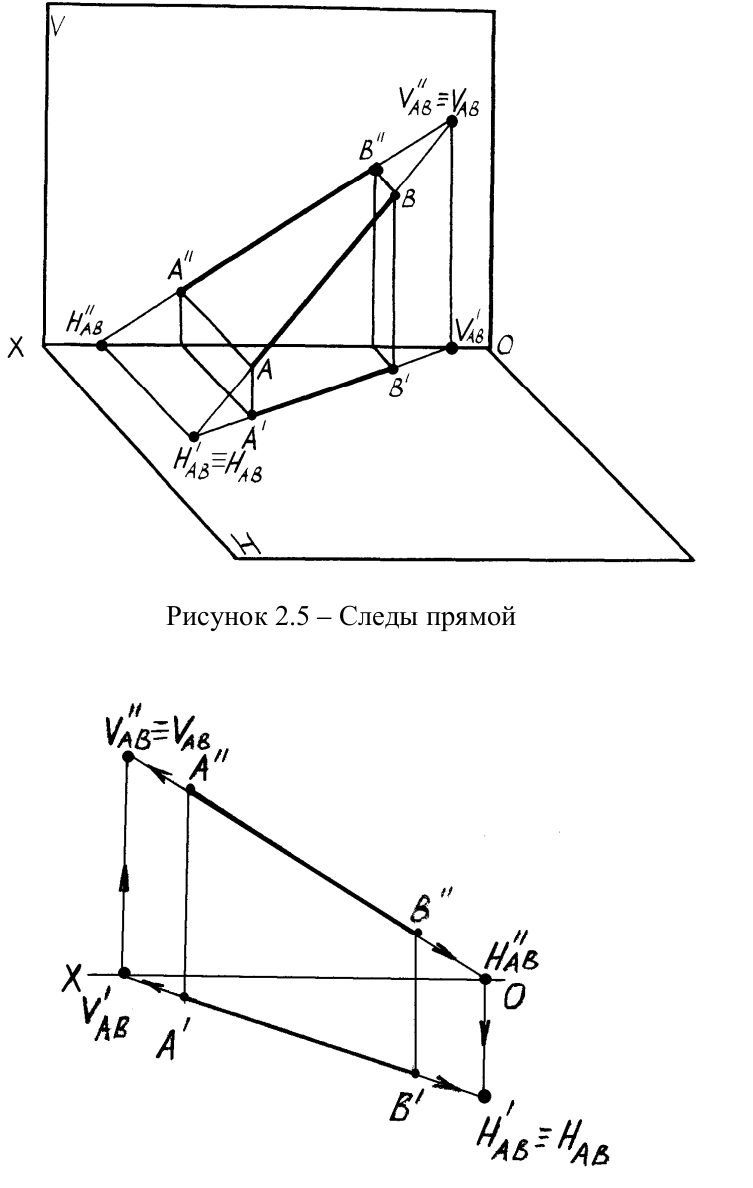
Рисунок 2.5 – Следы прямой

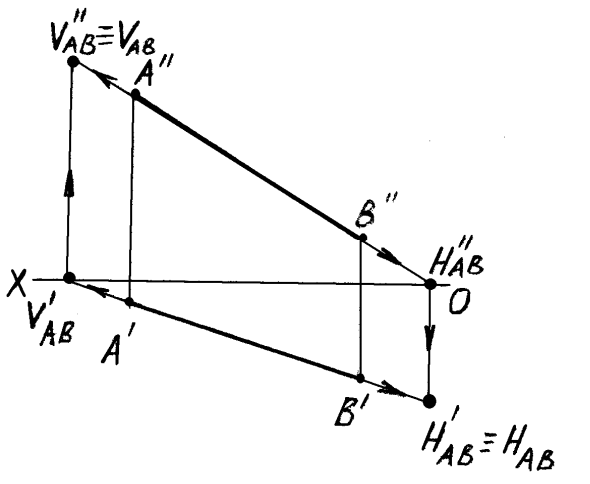
Рисунок 2.6 – Построение следов прямой

Из пространственных чертежей следует методика построения проекций следов прямой на эпюре (рисунок 2.6).