Взаимное положение двух прямых.

Две прямые линии в пространстве могут бытьпараллельными, пересекающимися и скрещивающимися. Их положение в пространстве устанавливается взаимным расположением одноименных проекций.

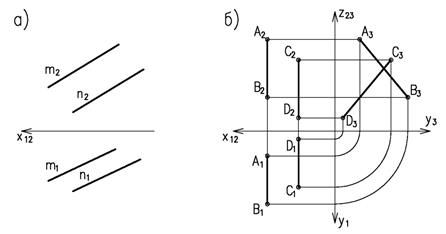
Если в пространстве две прямые параллельны, то их одноименные проекции также параллельны (рисунок 1.11а).

Параллельность профильных прямых не всегда очевидна. Хотя их горизонтальные и фронтальные проекции параллельны, сами прямые могут быть не параллельны. Для определения их взаимного положения можно построить профильную проекцию (рисунок 1.11б).

Пересекающиеся прямые – это прямые, имеющие общую точку, следовательно, если прямые в пространстве пересекаются, то точки пересечения их одноименных проекций лежат на одной линии проекционной связи (рисунок 1.12).

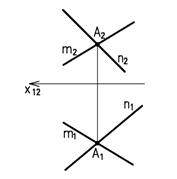
Рисунок 1.12

Скрещивающиеся прямыене имеют общей точки, поэтому точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рисунок 1.13).

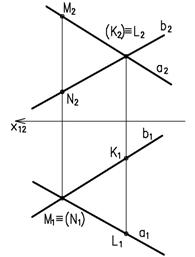Пары точек, у которых какие-либо одноименные проекции совпали, т.е. они лежат на одном проецирующем луче, называютсяконкурирующими (одна из них «закрывает» другую). Точки M и N – горизонтально-конкурирующие, точки K и L – фронтально-конкурирующие. Из двух конкурирующих точек видна та, у которой больше одна из координат (две другие совпадают).

Например, координата Z у точки М больше, чем у точки N , следовательно, прямая а в этом месте расположена выше прямой в и будет видима при взгляде сверху, т.е. на горизонтальной проекции. Аналогично, у точки L координата Y больше, чем у точки К, следовательно, в этом месте прямая а расположена ближе к зрителю и будет видима на фронтальной проекции. Определение видимости конкурирующих точек позволит нам в дальнейшем определять видимость прямой относительно плоскости.