Некоторые свойства центральной проекции

Любая точка местности М на снимке изображается точкой m (рис.1.3). Прямой линии на местности (K-L) в общем случае соответствует прямая (k-l) на снимке. В частном случае, когда прямая линия на местности (D-F) проходит через центр проекции S, она изображается на снимке в виде точки (df).

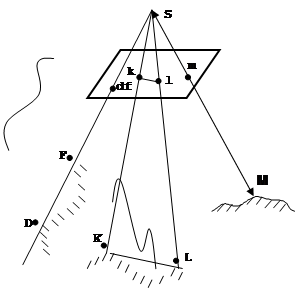Рис. 1.3

Точка надира n является точкой схода изображений на снимке вертикальных линий объекта (рис. 1.4)

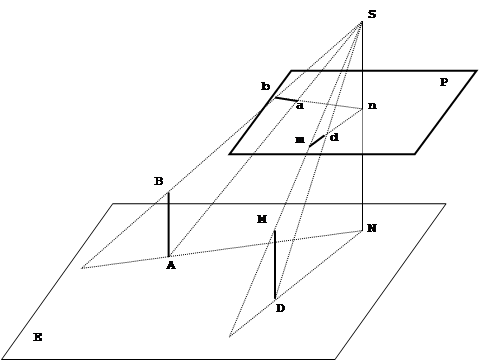
Рис. 1.4

Здесь AB и DM - вертикальные линии на объекте, а ab и dm – их изображения в плоскости снимка P. N – точка надира в предметной плоскости Е.

Если продолжить изображения вертикальных линий ab и dm, то они пересекутся в точке надира n. Для доказательства этого обстоятельства достаточно провести плоскости через вертикальные линии AB и DM и центр проекции S. Так как эти плоскости вертикальные, то они пересекутся по вертикальной линии SN, проходящей через центр проекции S и точку надира n(которая по определению является точкой пересечения плоскости снимка с отвесной линией, опущенной из центра проекции S). Очевидно, что изображения ab и dm вертикальных линий AB и DM находятся на следах пересечения плоскости снимка вертикальными плоскостями SAB и SDMипересекаются вточке надира n.

Линия действительного горизонтаii является геометрическим местом точек схода i изображений параллельных прямых линий объекта (рис. 1.5).

Построим изображение прямой АВ, расположенной в предметной плоскости Е. Для этого продолжим данную прямую до пересечения с осью перспективы ТТ(линия пересечения плоскости снимка с плоскостью объекта). Полученная таким образом точка Т является одновременно и изображением на снимке. Теперь продолжим линию АВ в обратном направлении до бесконечности. Очевидно, что проектирующий луч, идущий от бесконечно удаленной точки, лежащей на линии, параллелен этой линии и пересекает снимок в точке схода i, лежащей на линии действительного горизонта. Изображение линии на снимке получают в результате соединения точек i и Т.

Аналогично строят изображения других линий. Если они параллельны между собой в плоскости Е, то из изображения на снимке пересекаются в точке сходаi.

Рис. 1.5

Теория одиночного снимка

1.1

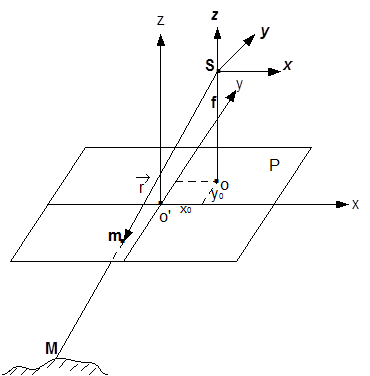Рис. 1.1.1

На каждом снимке имеются изображения координатных меток, которые определяют правую прямоугольную систему координат снимка o’xyz.

Ось х этой системы проходит через координатные метки 1-2 и направлена приблизительно по направлению полета. Началом системы координат является точка о’, получаемая в результате пересечения оси х с линией проведенной через координатные метки 3 и 4. Ось y лежит в плоскости снимка Р и перпендикулярна оси х. Ось z дополняет систему до правой.

Любая точка снимка, например m, имеет в этой системе координат координаты m(х,у,z =0). Центр проекции S имеет в этой системе координаты S ( x=x_0, y=y_0, z=f ).

f - фокусное расстояние снимка, а х₀ и у₀ – координаты главной точки снимка - О.

Для восстановления связки проектирующих лучей, сформировавших снимок в системе координат снимка o’xyz, необходимо для каждой точки снимка определить координаты вектора 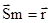в этой системе координат по измеренным на снимке координатам точки m.

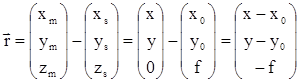. (1.1.1)

Из выражения (1.1.1) следует, что для восстановления связки проектирующих лучей, необходимо измерить координаты точки и знать значения координат центра проекции S в системе координат снимка f , х₀ , y₀, которые являются постоянными для данного снимка и называются элементами внутреннего ориентирования снимка.

Более широко в фотограмметрии используют систему координат снимка Sxyz , началом которой является центр проекции S, а оси координат параллельны соответствующим осям системы координат o’xyz.

Так как система координат Sxyz параллельна системе координат o’xyz, то, как известно из аналитической геометрии, координаты векторов в обеих системах координат равны, то есть координаты вектора 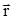в системе координат Sxyz определяется выражением (1.1.1).