Вторинна статистична обробка даних

До вторинних відносять такі методи статистичної обробки, за допомогою яких на базі первинних даних виявляють приховані в них статистичні закономірності. Вторинні методи можна поділити на способи оцінки значущості відмінностей і способи встановлення статистичних взаємозв'язків.

Способи оцінки значущості відмінностей. Для порівняння вибіркових середніх величин, що належать до двох сукупностей даних, і для вирішення питання про те, чи відрізняються середні значення статистично достовірно один від одного, використовують t – критерій Стьюдента. Його формула виглядає наступним чином:

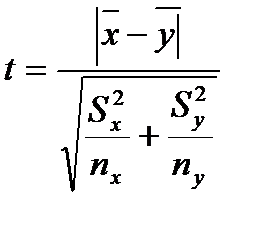
де S²_x, S²_y – вибіркові середні значення порівнюваних вибірок, n_x, n_y – інтегровані показники відхилень приватних значень з двох порівнюваних вибірок.

Після обчислення значення показника t за таблицею критичних значень заданого числа ступенів свободи (df = n_x + n_y – 2) і обраної ймовірності допустимої помилки (0,05, 0,01, 0,001 і т. п.) знаходять табличне значення t. Якщо вирахуване значення t більше або дорівнює табличному, роблять висновок про те, що порівнювані середні значення двох вибірок статистично достовірно відрізняються з імовірністю допустимої помилки, меншою або рівною обраній.

Якщо в процесі дослідження постає завдання порівняти неабсолютні середні величини, частотні розподілу даних, то використовується χ² критерій. Його формула виглядає наступним чином:

Для порівняння дисперсій двох вибірок використовується F – критерій Фішера. Його формула виглядає наступним чином:

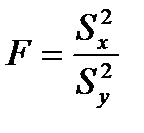
при цьому в чисельнику завжди повинна бути більша дисперсія, а в знаменнику менша.

df₁ – n-1

df₂ – n-1

Якщо вирахуване значення F більше або рівне табличному, роблять висновок про те, що відмінності дисперсій у двох вибірках статистично достовірні.

Способи встановлення статистичних взаємозв'язків. Попередні показники характеризують сукупність даних за якоюсь одною ознакою. Цю змінну ознаку називають змінною величиною або просто змінною. Міри зв'язку виявляють співвідношення між двома змінними або між двома вибірками. Ці зв'язки, або кореляції, визначають через обчислення коефіцієнту кореляції. Однак наявність кореляції не означає, що між змінними існує причинний (або функціональний) зв’язок. Функціональна залежність – це окремий випадок кореляції. Навіть якщо зв'язок причинний, кореляційні показники не можуть вказати, яка з двох змінних є причиною, а яка – наслідком. Крім того, будь-який виявлений в психологічних дослідженнях зв'язок, як правило, існує завдяки й іншим змінним, а не тільки двом розглянутим. До того ж взаємозв'язки психологічних ознак настільки складні, що їх обумовленість однією причиною навряд чи спроможна, вони детерміновані безліччю причин.

За щільністю зв'язку можна виділити наступні види кореляції: повна, висока, виражена, часткова; відсутність кореляції. Ці види кореляцій визначають залежно від значення коефіцієнту кореляції.

При повній кореляції його абсолютні значення дорівнюють або дуже близькі до 1. У цьому випадку встановлюється обов'язкова взаємозалежність між змінними. Тут імовірна функціональна залежність.

Висока кореляція встановлюється при абсолютному значень коефіцієнту 0,8 – 0,9. Виражена кореляція вважається при абсолютному значенні коефіцієнту 0,6 – 0,7. Часткова кореляція існує при абсолютному значенні коефіцієнту 0,4 – 0,5.

Абсолютні значення коефіцієнту кореляції менше 0,4 свідчать про дуже слабкий кореляційний зв'язок і, як правило, в розрахунок не приймаються. Відсутність кореляції констатується при значень коефіцієнту 0.

Крім того, в психології при оцінці щільності зв'язку використовують так звану «приватну» класифікацію кореляційних зв'язків. Вона орієнтована не на абсолютну величину коефіцієнтів кореляції, а на рівень значимості цієї величини при певному об’ємі вибірки. Ця класифікація застосовується при статистичній оцінці гіпотез. При цьому підході передбачається, що чим більша вибірка, тим менше значення коефіцієнту кореляції може бути прийняте для визнання достовірності зв'язків, а для малих вибірок навіть абсолютно велике значення коефіцієнту може виявитися недостовірним.

Заспрямованістю виділяють такі види кореляційних зв'язків: позитивний (прямий) і негативний (зворотний). Позитивний (прямий) кореляційний зв'язок реєструється при коефіцієнті зі знаком «плюс»: при збільшенні значення однієї змінної спостерігається збільшення іншої. Негативна (зворотна) кореляція має місце при значеннях коефіцієнту зі знаком «мінус». Це означає зворотну залежність: збільшення значення однієї змінної тягне за собою зменшення іншої.

За формою розрізняють такі види кореляційних зв'язків: прямолінійний і криволінійний. При прямолінійному зв'язку рівномірним змінам однієї змінної відповідають рівномірні зміни іншої. Якщо говорити не тільки про кореляцію, а й про функціональні залежності, то такі форми залежності називають пропорційними. У психології строго прямолінійні зв'язки – явище рідкісне. При криволінійному зв'язку рівномірна зміна однієї ознаки поєднується з нерівномірною зміною іншої. Ця ситуація для психології типова.

Коефіцієнт лінійної кореляції Пірсона (r_xy).

Коефіцієнт кореляції Пірсона називається також коефіцієнтом лінійної кореляції. Він дозволяє визначити силу зв'язку між двома ознаками, виміряними в метричних шкалах.

Вихідний принцип коефіцієнта кореляції Пірсона – використання моментів творення (відхилень значення змінної від середнього значення):

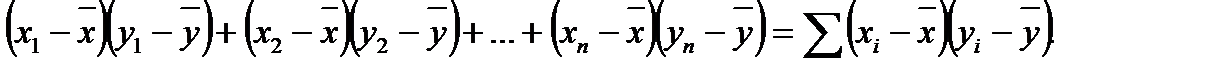
Якщо сума моментів творення велика і позитивна, то х і у зв'язані прямою залежністю; якщо сума велика і негативна, то х і у сильно пов'язані зворотною залежністю; нарешті, у разі відсутності зв'язку між x і у сума добутків моментів близька до нуля.

Для того щоб статистика не залежала від обсягу вибірки, береться не сума добутків моментів, а середнє значення. Однак поділ проводиться не на об’єм вибірки, а на число ступенів свободи n – 1.

Величина 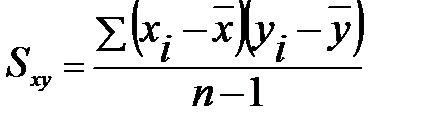є мірою зв’язку між x та y та називається коваріацією x та y.

Для того щоб стандартизувати міру зв'язку, необхідно позбавити коваріацію від впливу стандартних відхилень. Для цього треба розділити S_xy на S_x і S_y:

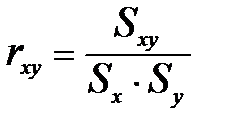
При порівнянні порядкових даних застосовується коефіцієнт рангової кореляції за Ч. Спірменом (R):

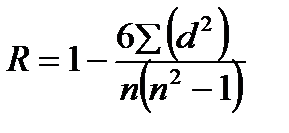
де d - різниця рангів (порядкових місць) двох величин, n - число порівнюваних пар величин двох змінних (X і Y).

Оцінка значущості коефіцієнту кореляції проводиться за таблицею.

Впровадження в наукових дослідженнях автоматизованих засобів обробки даних дозволяє швидко і точно визначати будь кількісні характеристики будь-яких масивів даних. Розроблено різні програми для комп'ютерів, за якими можна проводити відповідний статистичний аналіз практично будь-яких вибірок. З маси статистичних прийомів в психології найбільшого поширення набули такі: 1) комплексне обчислення статистик; 2) кореляційний аналіз; 3) дисперсійний аналіз; 4) регресійний аналіз; 5) факторний аналіз; 6) таксономічний (кластерний) аналіз; 7) шкалювання. Познайомитися з характеристиками цих методів можна в спеціальній літературі («Статистичні методи в педагогіці і психології» Стенлі Дж., Гласа Дж. (М., 1976), «Математична психологія» Г. В. Суходольського (СПб., 1997), «Математичні методи психологічного дослідження» А. Д. Наследова (СПб., 2005) та ін.).