Первинна статистична обробка даних
Всі методи кількісної обробки прийнято поділяти на первинні та вторинні.
Первинна статистична обробка націлена на упорядкування інформації про об’єкт і предмет вивчення. На цій стадії «сирі» відомості групуються за тими чи іншими критеріями, заносяться в зведені таблиці. Первинно оброблені дані, представлені у зручній формі, дають дослідникові в першому наближенні поняття про характер усієї сукупності даних в цілому: про їх однорідність – неоднорідність, компактність – розкиданість, чіткість – розмитість і т. п. Ця інформація добре прочитується з наочних форм представлення даних і дає відомості про їх розподіл.
В ході застосування первинних методів статистичної обробки виходять показники, безпосередньо пов'язані з виробленими в дослідженні вимірами.
До основних методів первинної статистичної обробки відносяться: обчислення заходів центральної тенденції та заходів рознесення (мінливості) даних.
Первинний статистичний аналіз всієї сукупності отриманих у дослідженні даних дає можливість охарактеризувати її в гранично стислому вигляді і відповісти на два головних питання: 1) яке значення найбільш характерне для вибірки; 2) чи велике рознесення даних щодо цього характерного значення, тобто яка «розмитість» даних. Для вирішення першого питання обчислюються міри центральної тенденції, для вирішення другого – міри мінливості (або рознесення). Ці статистичні показники використовуються у відношенні кількісних даних, представлених в порядкової, інтервальної або пропорційною шкалою.
Міри центральної тенденції – це величини, навколо яких групуються інші дані. Дані величини є як би узагальнюючими всю вибірку показниками, що, по-перше, дозволяє судити за ними про всю вибірку, а по-друге, дає можливість порівнювати різні вибірки, різні серії між собою. До мір центральної тенденції в обробці результатів психологічних досліджень відносяться: вибіркове середнє, медіана, мода.
Вибіркове середнє (М) – це результат ділення суми всіх значень (х) на їх кількість (n).
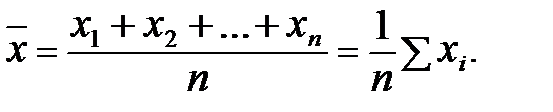
Медіана (Ме) – це значення, вище і нижче якого кількість відмінних значень однакова, тобто це центральне значення в послідовному ряду даних. Медіана не обов'язково повинна співпадати з конкретним значенням. Збіг відбувається у випадку непарного числа значень (відповідей), розбіжність – при парному їх числі. В останньому випадку медіана вираховується як середнє арифметичне двох центральних значень у впорядкованому ряді.
Мода (Мо) – це значення, яке найбільш часто зустрічається у вибірці, тобто значення з найбільшою частотою. Якщо всі значення в групі зустрічаються однаково часто, то вважається, що моди немає. Якщо два сусідніх значення мають однакову частоту і більші частоти будь-якого іншого значення, мода є середнє цих двох значень. Якщо те ж саме відноситься до двох несуміжних значень, то існує дві моди, а група оцінок є бімодальною.
Зазвичай вибіркове середнє (середнє арифметичне) застосовується при прагненні до найбільшої точності у визначенні центральної тенденції. Медіана обчислюється в тому випадку, коли в серії є «нетипові» дані, які різко впливають на середнє. Мода використовується в ситуаціях, коли не потрібна висока точність, але важлива швидкість визначення міри центральної тенденції.
Обчислення всіх трьох показників проводиться також для оцінки розподілу даних. При нормальному розподілі значення вибіркового середнього, медіани і моди однакові або дуже близькі.
Міри рознесення(мінливості) – це статистичні показники, що характеризують відмінності між окремими значеннями вибірки. Вони дозволяють судити про ступінь однорідності отриманої множинності, її компактності, а опосередковано і про надійність отриманих даних та результатів, які з неї випливають. Найбільш використовувані в психологічних дослідженнях показники: середнє відхилення, дисперсія, стандартне відхилення.
Розмах (ρ) – це інтервал між максимальним і мінімальним значеннями ознаки. Визначається легко і швидко, але чутливий до випадковостей, особливо при малому числі даних.
Середнє відхилення (МД) – це середньоарифметичне різниці (за абсолютною величиною) між кожним значенням у вибірці і її середнім.
де d = | Х – М |, М – середнє вибірки, X – конкретне значення, n – число значень.
Безліч всіх конкретних відхилень від середнього характеризує мінливість даних, але якщо не взяти їх за абсолютною величиною, то їх сума дорівнюватиме нулю і ми не отримаємо інформації про їх мінливість. Середнє відхилення показує ступінь скупченості даних навколо вибіркового середнього. До речі, іноді при визначенні цієї характеристики вибірки замість середнього (М) беруть інші міри центральної тенденції – моду або медіану.
Дисперсія (S2) характеризує відхилення від середньої величини в даній вибірці. Обчислення дисперсії дозволяє уникнути нульової суми конкретних різниць (d = X – М) не через їх абсолютні величини, а через їх зведення до квадрату:
 для великих вибірок (n ˃ 30)
для великих вибірок (n ˃ 30)
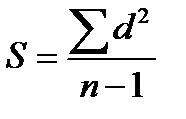 для малих вибірок (n ˂ 30)
для малих вибірок (n ˂ 30)
де d = | Х – М |, М – середнє вибірки, X – конкретне значення, N – число значень.

Стандартне відхилення (S). Через піднесення до квадрату окремих відхилень d при вирахуванні дисперсії отримана величина виявляється далекою від первинних відхилень і тому не дає про них наочного уявлення. Щоб цього уникнути і отримати характеристику, яку можна порівняти з середнім відхиленням, проробляють зворотну математичну операцію – з дисперсії витягують квадратний корінь. Її позитивне значення і приймається за міру мінливості, названу середньоквадратичним, або стандартним, відхиленням:
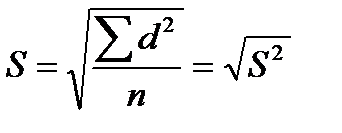 для великих вибірок (n ˃ 30)
для великих вибірок (n ˃ 30)
 для малих вибірок (n ˂ 30)
для малих вибірок (n ˂ 30)
де d = | Х – М |, М – середнє вибірки, X – конкретне значення, n – число значень.
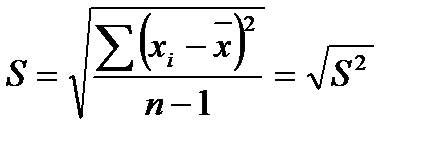
Дата добавления: 2015-10-09; просмотров: 3675;
