Напряженное и деформированное состояние в точке. Метод сечений
Тема 2. Внутренние силовые факторы, их определение, понятия о напряжениях, деформациях и методах расчета на прочность
Напряженное и деформированное состояние в точке. Метод сечений
Под действием внешних сил все тела меняют свою форму - деформируются. При нагружении твердого тела в нем возникают внутренние силы взаимодействия между частицами (атомами, молекулами), оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое те занимали до деформации. Мерой интенсивности внутренних сил является физическая величина, которая называется напряжением.
В сопротивлении материалов не рассматривают начальные внутренние силы в теле (в ненагруженном состоянии), а изучают дополнительные внутренние силы, которые появляются в результате нагружения тела внешними силами. Внутренние силы часто называются усилиями. Для решения задачи о прочности надо уметь определять внутренние силы. Для этого в сопротивлении материалов широко применяют метод сечений (рис. 2.1).
Суть метода сечений заключается в следующем. Рассматривается тело нагруженное некоторой системой внешних сил Р1, Р2,…,РN. Так как мы решаем статическую задачу, то будем полагать, что под действием заданной системы внешних сил тело находится в состоянии равновесии. Произвольной секущей плоскостью Т мысленно разделим исходное тело на две части А и В. В этом случае в секущей плоскости действует некоторая самоуравновешенная система внутренних сил, которые по отношению к частям А и В являются условно внешними. Так как мысленное рассечение тела на части не отменяет условия его равновесия, то новая система сил, действующих на части А и В также должна быть самоуравновешенной. Распределенные по секущей плоскости элементарные внутренние силы, используя методы теоретической механики, можно привести к главному вектору внутренних сил РВН и главному моменту внутренних сил МВН. Данные эквивалентные внутренние силы совместно с внешними силами обеспечивают равновесие отсеченной части тела, а значит, составив уравнения его равновесия можно найти неизвестные внутренние силы: главный вектор внутренних сил РВН и главный момент внутренних сил МВН.
Выделим в рассматриваемом сечении с единичным вектором нормали  около точки К малую площадку
около точки К малую площадку  (рис. 2.2а). Главный вектор внутренних сил, действующих на этой элементарной площадке
(рис. 2.2а). Главный вектор внутренних сил, действующих на этой элементарной площадке 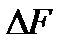 , обозначим через
, обозначим через 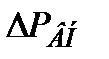 . В общем случае напряжения, как мера интенсивности внутренних сил, по данной площадке распределены неравномерно, однако, уменьшая величину площадки
. В общем случае напряжения, как мера интенсивности внутренних сил, по данной площадке распределены неравномерно, однако, уменьшая величину площадки 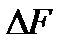 , можно степень неравномерности этого распределения уменьшить. Среднее напряжение на площадке
, можно степень неравномерности этого распределения уменьшить. Среднее напряжение на площадке 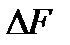 тогда будет
тогда будет
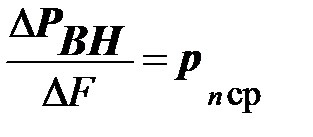 .
.
В пределе при 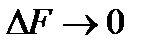 получим полное напряжение в точке К
получим полное напряжение в точке К
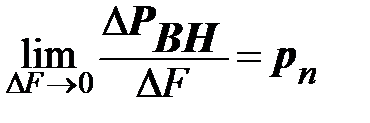 .
.
Вектор полных напряжений 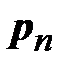 зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки
зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки 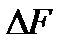 , характеризуемой вектором
, характеризуемой вектором  . Совокупность всех векторов напряжений в точке К для всевозможных направлений вектора
. Совокупность всех векторов напряжений в точке К для всевозможных направлений вектора  определяет напряженное состояние в точке К.
определяет напряженное состояние в точке К.
Рис.2.1. Метод сечений
В общем случае направление вектора полных напряжений 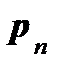 не совпадает с направлением вектора нормали
не совпадает с направлением вектора нормали 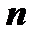 . Проекции вектора
. Проекции вектора 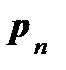 на направление нормали к площадке называется нормальным напряжением
на направление нормали к площадке называется нормальным напряжением  , а на плоскость, проходящую через точку К и ортогональную вектору
, а на плоскость, проходящую через точку К и ортогональную вектору 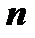 - касательным напряжением
- касательным напряжением 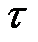 (рис. 2.2б).
(рис. 2.2б).
Рис. 2.2: а — напряжение в сечении тела, б — нормальные s и касательные t напряжения в сечении тела
Нормальное напряжение считается положительным, если оно направлено от площадки (на растяжение). Напряжение в системе единиц СИ измеряется в Паскалях (Па): 1Па 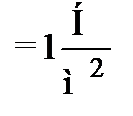 .
.
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела. Деформация тела может быть упругой, исчезающей после снятия нагрузки, и пластической-остаточные (не исчезающие) деформации.
Отнесем недеформированное состояние тела к декартовой системе координат 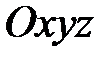 (рис. 2.3).
(рис. 2.3).
| Деформированное
состояние тела
|
| Недеформированное
состояние тела
|
Рис. 2.3. К определению деформации тела
Положение некоторой точки 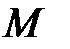 в недеформированном состоянии тела определяется радиус-вектором
в недеформированном состоянии тела определяется радиус-вектором 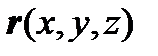 . После деформации тела точка
. После деформации тела точка 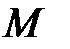 занимает положение
занимает положение 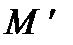 , характеризуемое радиус-вектором
, характеризуемое радиус-вектором 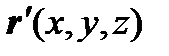 . Вектор
. Вектор 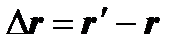 называется вектором перемещения точки
называется вектором перемещения точки 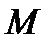 . Проекции вектора
. Проекции вектора 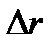 на координатные оси определяют компоненты перемещений
на координатные оси определяют компоненты перемещений 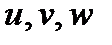 соответственно вдоль осей
соответственно вдоль осей 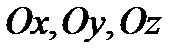 .
.
Интенсивность изменения формы и размеров твердого тела характеризуется физической величиной, которая называется деформацией (не путать с самим явлением изменения формы и размеров, которое тоже называют деформацией). Деформация подразделяется на линейную(рис. 2.4 слева) и угловую(рис. 2.4 справа). Угловую деформацию часто называют деформацией сдвига или углом сдвига.
Рис. 2.4. К определению линейной и угловой деформаций в точке А
Числовое значение деформации определяется по приведенным ниже формулам, и, очевидно, является безразмерной величиной:
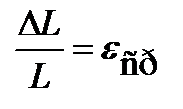 - средняя относительная линейная деформация по направлению AB;
- средняя относительная линейная деформация по направлению AB;
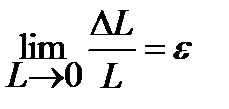 - относительная линейная деформация в точке по направлению AB;
- относительная линейная деформация в точке по направлению AB;
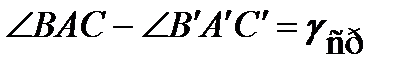 - средняя относительная угловая деформация в плоскости ABC;
- средняя относительная угловая деформация в плоскости ABC;
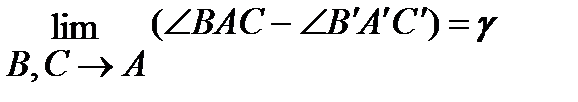 -относительная угловая деформация в точке в плоскости ABC.
-относительная угловая деформация в точке в плоскости ABC.
Таким образом, линейная деформация показывает интенсивность изменения длины (положительна при увеличении длины), а угловая - изменение угла, до деформации бывшего прямым (положительна при уменьшении угла).
Совокупность деформаций в точке A по всевозможным направлениям определяет деформированное состояние в точке A. Напряженное и деформированное состояния, рассматриваемые вместе и во взаимосвязи - это напряженно-деформированное состояние (НДС) в данной точке.
Можно доказать, что для нахождения напряжений и деформаций на любой площадке и по любому направлению в данной точке, достаточно знать:
1. Нормальные и касательные напряжения по направлению координатных осей (рис.2.5)
Рис. 2.5. Нормальные и касательные напряжения в окрестности точки А
2. Линейные деформации по направлению координатных осей и угловые деформации в соответствующих координатных плоскостях.
Эти величины образуют соответственно тензор напряжений:

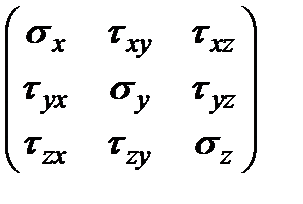 ,
,
и тензор деформаций:
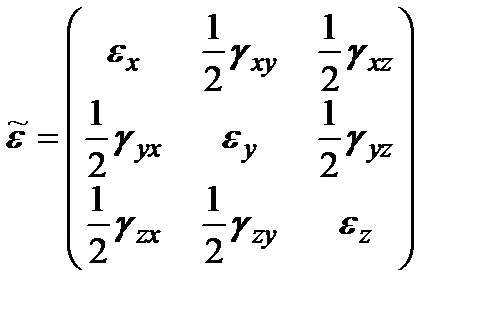 .
.
в данной точке упругого тела.
При малых деформациях (при использовании предположений, характерных для сопротивления материалов) напряжения и деформации связаны между собой линейными соотношениями (выполняется так называемый обобщенный закон Гука)
В более подробных курсах сопротивления материалов выводятся также соотношения между деформациями и перемещениями в точке (соотношения Коши):

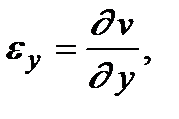
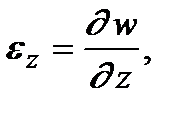
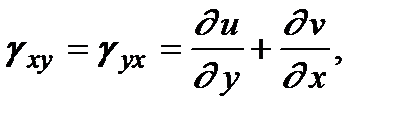
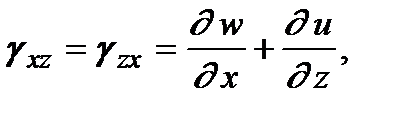
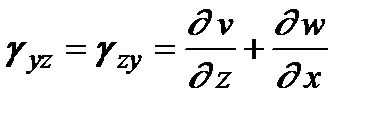 .
.
Величина нормальных 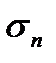 и касательных
и касательных 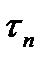 напряжений, действующих на площадке с вектором нормали
напряжений, действующих на площадке с вектором нормали 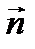 , зависит от ее ориентации. Среди всех возможных направлений вектора нормали
, зависит от ее ориентации. Среди всех возможных направлений вектора нормали 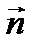 , а значит, положения площадки, существует такое направление, при котором полный вектор напряжений
, а значит, положения площадки, существует такое направление, при котором полный вектор напряжений 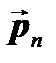 будет параллелен вектору нормали
будет параллелен вектору нормали 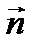 . На такой площадке будут действовать только нормальные напряжения, а касательные напряжения будут отсутствовать. Кроме того, среди множества площадок, проходящих через точку тела, всегда можно провести три взаимно перпендикулярные площадки, касательные напряжения на которых будут равны нулю.
. На такой площадке будут действовать только нормальные напряжения, а касательные напряжения будут отсутствовать. Кроме того, среди множества площадок, проходящих через точку тела, всегда можно провести три взаимно перпендикулярные площадки, касательные напряжения на которых будут равны нулю.
Площадки, на которых касательные напряжения отсутствуют, называются главными, а действующие на этих площадках нормальные напряжения ¾ главными нормальными напряжениями. Как будет выяснено ниже, по величине главных напряжений можно судить о близости наступления предельного состояния (разрушения) в данной точке.
Направления нормалей к этим площадкам называются главными направлениями или главными осями.
Главные напряжения принято обозначать 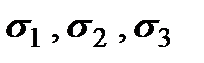 . Индексы надо расставлять так, чтобы выполнялось неравенство:
. Индексы надо расставлять так, чтобы выполнялось неравенство:  (с учетом знаков напряжений). Главные напряжения обладают важным свойством: нормальные напряжения
(с учетом знаков напряжений). Главные напряжения обладают важным свойством: нормальные напряжения 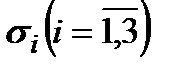 на главных площадках принимают экстремальные значения (
на главных площадках принимают экстремальные значения ( 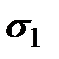 - наибольшее из всех возможных нормальных напряжений в данной точке, а
- наибольшее из всех возможных нормальных напряжений в данной точке, а  - наименьшее).
- наименьшее).
Итак, напряженное состояние в любой точке может быть охарактеризовано тремя главными напряжениями, действующими по трем взаимно перпендикулярным направлениям. В частных случаях одно или два главных нормальных напряжения могут быть равными нулю. В зависимости от числа действующих главных нормальных напряжений различают три вида напряженных состояний в точке: линейное (одноосное) (рис. 2.6а), плоское (двухосное) (рис. 2.6б) и объемное (трехосное) (рис. 2.6в).
Рис. 2.6. Типы напряженных состояний: одноосное (а), двухосное (б) и трехосное (в)
Дата добавления: 2015-09-07; просмотров: 2088;
 около точки К малую площадку
около точки К малую площадку  (рис. 2.2а). Главный вектор внутренних сил, действующих на этой элементарной площадке
(рис. 2.2а). Главный вектор внутренних сил, действующих на этой элементарной площадке 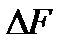 , обозначим через
, обозначим через 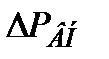 . В общем случае напряжения, как мера интенсивности внутренних сил, по данной площадке распределены неравномерно, однако, уменьшая величину площадки
. В общем случае напряжения, как мера интенсивности внутренних сил, по данной площадке распределены неравномерно, однако, уменьшая величину площадки 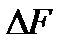 , можно степень неравномерности этого распределения уменьшить. Среднее напряжение на площадке
, можно степень неравномерности этого распределения уменьшить. Среднее напряжение на площадке 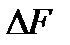 тогда будет
тогда будет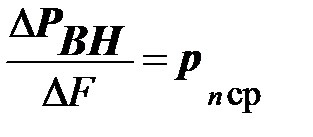 .
.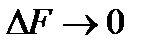 получим полное напряжение в точке К
получим полное напряжение в точке К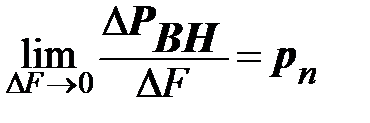 .
.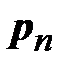 зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки
зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки 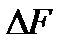 , характеризуемой вектором
, характеризуемой вектором  . Совокупность всех векторов напряжений в точке К для всевозможных направлений вектора
. Совокупность всех векторов напряжений в точке К для всевозможных направлений вектора  определяет напряженное состояние в точке К.
определяет напряженное состояние в точке К.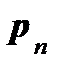 не совпадает с направлением вектора нормали
не совпадает с направлением вектора нормали 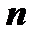 . Проекции вектора
. Проекции вектора 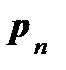 на направление нормали к площадке называется нормальным напряжением
на направление нормали к площадке называется нормальным напряжением  , а на плоскость, проходящую через точку К и ортогональную вектору
, а на плоскость, проходящую через точку К и ортогональную вектору 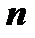 - касательным напряжением
- касательным напряжением 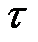 (рис. 2.2б).
(рис. 2.2б).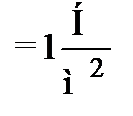 .
.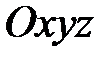 (рис. 2.3).
(рис. 2.3).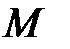 в недеформированном состоянии тела определяется радиус-вектором
в недеформированном состоянии тела определяется радиус-вектором 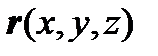 . После деформации тела точка
. После деформации тела точка 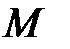 занимает положение
занимает положение 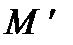 , характеризуемое радиус-вектором
, характеризуемое радиус-вектором 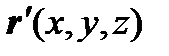 . Вектор
. Вектор 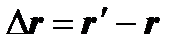 называется вектором перемещения точки
называется вектором перемещения точки 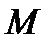 . Проекции вектора
. Проекции вектора 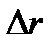 на координатные оси определяют компоненты перемещений
на координатные оси определяют компоненты перемещений 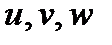 соответственно вдоль осей
соответственно вдоль осей 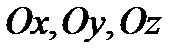 .
.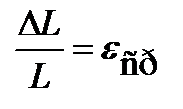 - средняя относительная линейная деформация по направлению AB;
- средняя относительная линейная деформация по направлению AB;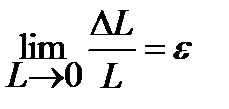 - относительная линейная деформация в точке по направлению AB;
- относительная линейная деформация в точке по направлению AB;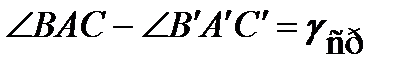 - средняя относительная угловая деформация в плоскости ABC;
- средняя относительная угловая деформация в плоскости ABC;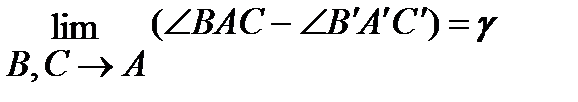 -относительная угловая деформация в точке в плоскости ABC.
-относительная угловая деформация в точке в плоскости ABC.
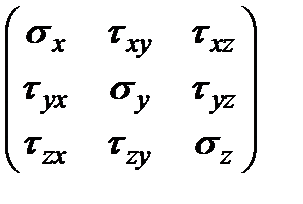 ,
,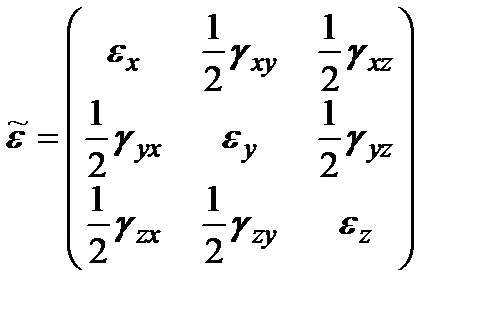 .
.
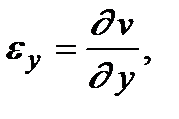
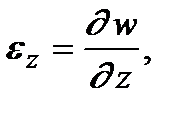
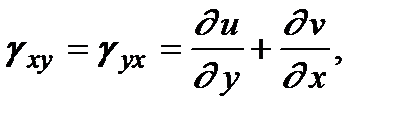
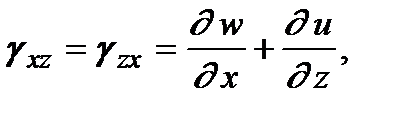
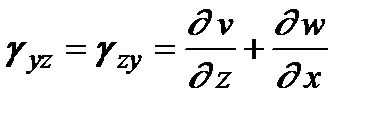 .
.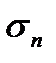 и касательных
и касательных 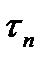 напряжений, действующих на площадке с вектором нормали
напряжений, действующих на площадке с вектором нормали 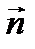 , зависит от ее ориентации. Среди всех возможных направлений вектора нормали
, зависит от ее ориентации. Среди всех возможных направлений вектора нормали 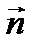 , а значит, положения площадки, существует такое направление, при котором полный вектор напряжений
, а значит, положения площадки, существует такое направление, при котором полный вектор напряжений 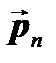 будет параллелен вектору нормали
будет параллелен вектору нормали 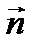 . На такой площадке будут действовать только нормальные напряжения, а касательные напряжения будут отсутствовать. Кроме того, среди множества площадок, проходящих через точку тела, всегда можно провести три взаимно перпендикулярные площадки, касательные напряжения на которых будут равны нулю.
. На такой площадке будут действовать только нормальные напряжения, а касательные напряжения будут отсутствовать. Кроме того, среди множества площадок, проходящих через точку тела, всегда можно провести три взаимно перпендикулярные площадки, касательные напряжения на которых будут равны нулю.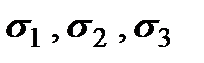 . Индексы надо расставлять так, чтобы выполнялось неравенство:
. Индексы надо расставлять так, чтобы выполнялось неравенство:  (с учетом знаков напряжений). Главные напряжения обладают важным свойством: нормальные напряжения
(с учетом знаков напряжений). Главные напряжения обладают важным свойством: нормальные напряжения 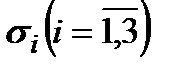 на главных площадках принимают экстремальные значения (
на главных площадках принимают экстремальные значения ( 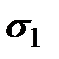 - наибольшее из всех возможных нормальных напряжений в данной точке, а
- наибольшее из всех возможных нормальных напряжений в данной точке, а  - наименьшее).
- наименьшее).