Внутренние силовые факторы
Как было показано в п.2.1 действие распределенных по секущей поверхности Т внутренних сил (рис. 2.1) можно привести к эквивалентной системе, когда в сечении действует главный вектор внутренних сил 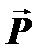 и главный момент
и главный момент 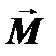 . Если главный вектор
. Если главный вектор 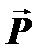 и главный момент
и главный момент 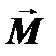 внутренних сил разложить по осям координат Ох,Оy и Оz, то в общем случае с каждой стороны от сечения получим шесть внутренних интегральных (суммарных) силовых факторов: три силы
внутренних сил разложить по осям координат Ох,Оy и Оz, то в общем случае с каждой стороны от сечения получим шесть внутренних интегральных (суммарных) силовых факторов: три силы 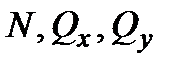 и три момента
и три момента 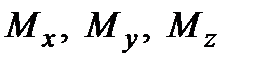 (рис. 2.7):
(рис. 2.7): 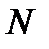 - продольная или нормальная сила;
- продольная или нормальная сила; 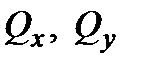 - поперечные (перерезывающие) силы;
- поперечные (перерезывающие) силы; 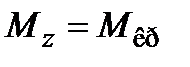 - крутящий момент;
- крутящий момент; 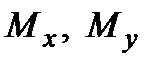 - изгибающие моменты. Заметим, что внутренние силовые факторы имеют ярко выраженный физический смысл; каждому из них соответствует определенный вид деформации стержня (балки): продольной силе
- изгибающие моменты. Заметим, что внутренние силовые факторы имеют ярко выраженный физический смысл; каждому из них соответствует определенный вид деформации стержня (балки): продольной силе 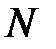 - деформация растяжения (сжатия); поперечным силам - деформация сдвига (среза); крутящему моменту - кручения; изгибающим моментам - изгиба.
- деформация растяжения (сжатия); поперечным силам - деформация сдвига (среза); крутящему моменту - кручения; изгибающим моментам - изгиба.
Рис. 2.7. Внутренние силовые факторы
Любая из отсеченных частей должна находиться в равновесии под действием внешних сил с одной стороны от сечения и внутренних силовых факторов. Запишем уравнения равновесия (уравнения статики) для левой (индекс «л») отсеченной части A в предположении, что на данную часть тела действует n внешних сил (на рис. 2.7 n=2):
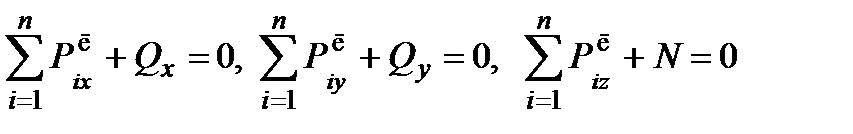
 .
.
Решив эти шесть уравнений, найдем внутренние силовые факторы в любом сечении стержня. Важно понимать, что внутренние силовые факторы заменяют действие мысленно отброшенной части стержня. Так как по третьему закону Ньютона правая часть действует на левую так же, как и левая на правую, то внутренние силовые факторы можно определять из равновесия любой (правой или левой) части стержня, находящегося в равновесии.
Дата добавления: 2015-09-07; просмотров: 1527;
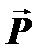 и главный момент
и главный момент 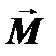 . Если главный вектор
. Если главный вектор 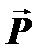 и главный момент
и главный момент 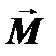 внутренних сил разложить по осям координат Ох,Оy и Оz, то в общем случае с каждой стороны от сечения получим шесть внутренних интегральных (суммарных) силовых факторов: три силы
внутренних сил разложить по осям координат Ох,Оy и Оz, то в общем случае с каждой стороны от сечения получим шесть внутренних интегральных (суммарных) силовых факторов: три силы 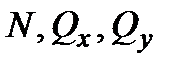 и три момента
и три момента 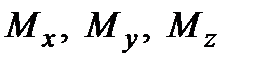 (рис. 2.7):
(рис. 2.7): 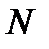 - продольная или нормальная сила;
- продольная или нормальная сила; 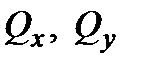 - поперечные (перерезывающие) силы;
- поперечные (перерезывающие) силы; 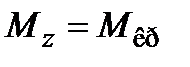 - крутящий момент;
- крутящий момент; 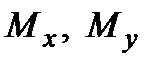 - изгибающие моменты. Заметим, что внутренние силовые факторы имеют ярко выраженный физический смысл; каждому из них соответствует определенный вид деформации стержня (балки): продольной силе
- изгибающие моменты. Заметим, что внутренние силовые факторы имеют ярко выраженный физический смысл; каждому из них соответствует определенный вид деформации стержня (балки): продольной силе 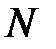 - деформация растяжения (сжатия); поперечным силам - деформация сдвига (среза); крутящему моменту - кручения; изгибающим моментам - изгиба.
- деформация растяжения (сжатия); поперечным силам - деформация сдвига (среза); крутящему моменту - кручения; изгибающим моментам - изгиба.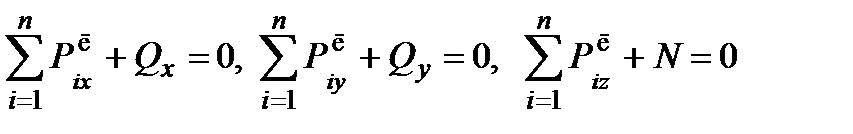
 .
.