Настройка регуляторов в системе подчиненного регулирования
Из ТАУ известно, что характер переходных процессов замкнутой системы определяется соотношением постоянных времени системы, и оптимальному переходному процессу соответствуют оптимальные постоянные времени. Математически это выражается определенным соотношением коэффициентов характеристического уравнения системы.
При этом переходной процесс в СУ по управляющему воздействию будет технически оптимальным. Заданная исходная система всегда обладает оптимальным соотношением постоянных времени, поэтому, используя коррекцию, нужно изменять постоянную времени системы, т.е. для настройки контура на технический оптимум подобрать такой тип регулятора с такими параметрами, чтобы получить характеристическое уравнение системы.
Рассмотрим, как проводится расчет настройки регулятора на примере контура регулирования тока якоря ДПТ в системе ТП-Д. Расчет производится для неподвижного якоря или при выключенном возбуждении.
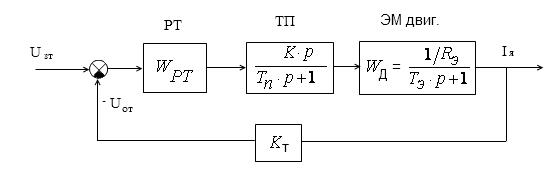
В контуре тока имеются 2 инерционности, характеризуемые постоянными времени:
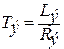 - электромагнитная постоянная времени якорной цепи.
- электромагнитная постоянная времени якорной цепи.
Tп – постоянная времени, отражающая инерционность фазового управления выпрямителем, запаздывание преобразователя, инерционность датчика и регулятора.
Tп – некомпенсированная постоянная времени 0,004÷0,01с
Tп <Tэ
При этом Tп называют большой постоянной времени, которую необходимо компенсировать.
Передаточная функция преобразователя и якорной цепи определяется:
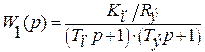
Используя ПИ-регулятор с передаточной функцией:
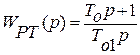
Получим передаточную функцию разомкнутой системы:

C целью компенсации большой постоянной времени контура примем To=Tэ, тогда передаточная функция для разомкнутого контура будет иметь вид:
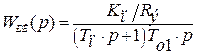
Передаточная функция замкнутого контура определяется:
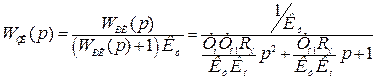
Замкнутый контур имеет систему 2го порядка.
Для того, чтобы получить в этой системе оптимальный переходной процесс, нужно чтобы коэффициент затухания (коэффициент демпфирования) был равен 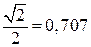 . В этом случае обеспечивается требуемый технический, оптимальный переходной процесс. Это условие будет выполнено, если коэффициент при операторе Лапласа «р» характеристического уравнения будет
. В этом случае обеспечивается требуемый технический, оптимальный переходной процесс. Это условие будет выполнено, если коэффициент при операторе Лапласа «р» характеристического уравнения будет  =>
=> 
Из параметров ПИ регулятора мы имеем:
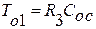

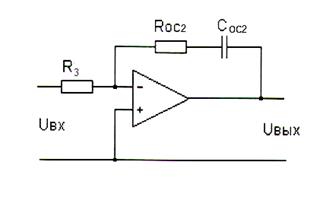
Тогда передаточная функция регулятора тока:
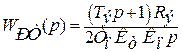
где 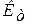 - коэффициент обратной связи по току, который определяется
- коэффициент обратной связи по току, который определяется

При таком регулировании тока передаточная функция замкнутого контура:
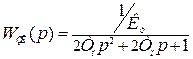
Получилось характеристическое уравнение контура с оптимальным соотношением коэффициентом. Поэтому переходной процесс РТ при выборе настройки контура будет оптимальным.
Получается настройка контура тока сохранится и при вращающемся якоре, когда проявится влияние ЭДС двигателя. Так как электромеханическая постоянная времени - Тм во много раз больше электромагнитной постоянной времени - Тэ (Тм>2Тэ) и Тп (Тм>>Tп), это влияние на переходной процесс в контуре тока оказывается не существенным.
Произведем расчет настройки регулятора контура скорости. В этом случае регулятор выбираем П или ПИ.
П-регулятор выбирается при малом диапазоне регулирования скорости. Коэффициент усиления регулятора и его параметры при настройке на технический оптимум по управляющему воздействию определяется:

С=Сд·Ф – конструктивный коэффициент двигателя.
При этом характеристическое уравнение получается 3го порядка, а переходной процесс с большим перерегулированием и временем большим, чем в контуре тока.
Отношение статического падения угловой скорости в системе с П-регулятором к статическому падению угловой скорости в разомкнутой системе определяется, как:

При Тм<4Тп статический перепад угловой скорости будет больше, чем в разомкнутой системе.
Чем больше Тм, тем больше Кос (коэффициент обратной связи по скорости), тем меньше статическое падение угловой скорости.
Действие П-регулятора сводится к следующему: при увеличении момента нагрузки на валу, скорость двигателя снижается, увеличивается сигнал с выхода регулятора скорости, т.е. увеличивается задание по контуру тока, возрастает ЭДС преобразователя и увеличивается ток я в якорной цепи. Чем меньше Кос, тем больше должна быть ошибка по скорости при одном и том же моменте нагрузки.
Дата добавления: 2015-10-09; просмотров: 4048;
