Ускорение. Равноускоренное прямолинейное движение. Графики зависимости кинематических величин от времени в равноускоренном движении.

Движение любого тела в реальных условиях никогда не бывает строго равномерным и прямолинейным. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением.

Ускорение – это величина, которая определяет быстроту изменения скорости тела, и равна пределу, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

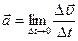
Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения за любые равные промежутки времени скорость увеличивается на одну и ту же величину и направление ускорения совпадает с направлением скорости движения.

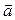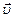­­ ∆ и а > 0

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

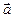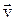­¯ ∆ и а ˂ 0

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Измеряют ускорение в метрах на секунду в квадрате

(м /с²).

При равноускоренном движении с начальной скоростью 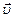₀ ускорение 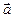равно .

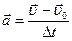где 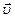– скорость в момент времени t, тогда скорость равнопеременного движения равна

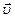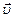= ₀ + 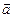t илиυ=±υ₀±at(3.3)

Пройденный путь при прямолинейном равноускоренном движении равен модулю перемещения и определяется по формуле:

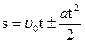(3.4)

где знак “плюс” относится к ускоренному, а “минус” – к замедленному движению.

Если время движения тела неизвестно, можно использовать другую формулу перемещения:

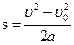(3.5)

где υ – конечная скорость движения;

υ₀– начальная скорость движения

Координаты тела при равноускоренном движении в любой момент времени можно определить по формулам:

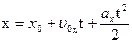
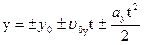
где х₀ ; у₀ – начальные координаты тела; υ₀-скорость тела в начальный момент времени; а – ускорение движения. Знак «+» и «-» зависят от направления оси ОХ и направления векторов 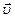и .

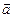Проекция перемещение

на ось ОХ равна: S_х = х-х₀

на ось ОУ равна: S_у = у-у₀

График зависимости перемещения тела от времени при

υ₀ = 0 показан на рис. 1.9.

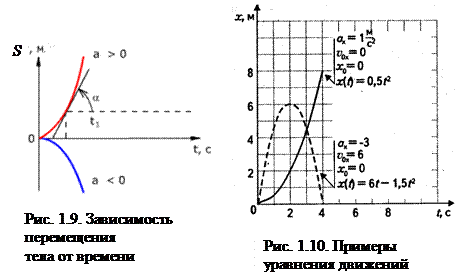
Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени υ=tgα.

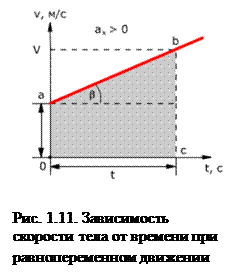Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При

а < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.10).

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия

(рис. 1.11). Тангенс угла наклона прямой к оси времени численно равен ускорению.

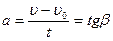
При этом перемещение численно равно площади фигуры 0abc (рис. 1.11). Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: 0a = υ₀ bc = υ.

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна: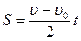

Учитывая, что υ= υ₀+at, получим

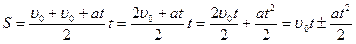
Получили формулу нахождения пути при равнопеременном движении.

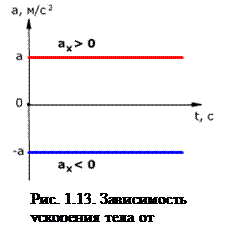
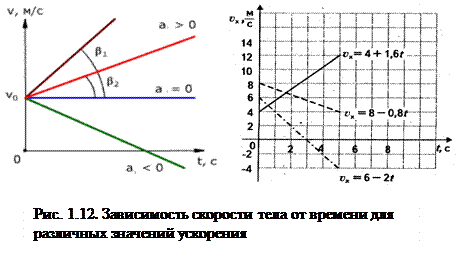
График зависимости скорости тела от времени при

различных ускорениях показан на рис. 1.12.