Движение тела брошенного вертикально вверх.
Тело, брошенное вертикально вверх движется равномернозамедленно до тех пор, пока скорость его не станет равной нулю. В этот момент тело достигает максимальной высоты и начинает свободно падать, двигаясь обратно вниз равноускоренно.
Для тела, брошенного вертикально вверх: начальная скорость, с которой тело брошено вверх, равна его конечной скорости при соприкосновении с землёй. Время подъёма равно времени падения.
Если вектор начальной скорости υ0 направлен по вертикали, либо υ0 = 0, то свободное падение является прямолинейным движением. В этом случае для нахождения скорости и пути применяются все формулы ( 3.3 – 3.5) для равноускоренного прямолинейного движения.
Только в этих формулах S обычно заменяется высотой h., а ускорение движение а – ускорением свободного падения g и υ0 = 0.
υ=±υ0±gt(3.3)
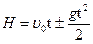 (3.4)
(3.4)
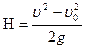 (3.5)
(3.5)
Координаты тела в любой момент времени можно определить по формулам:
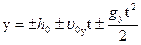
Если ось OY направлена вниз, то проекция ускорения свободного падения gy на эту ось положительна. Если ось OY направлена вверх, то проекция gy отрицательна. Например, мяч, подброшенный вертикально вверх, до верхней точки подъёма движется равнозамедленно, а его движение вниз будет равноускоренным.
Проекции начальной υoy и конечной υy скоростей положительны, если направление скоростей совпадает с направлением оси OY, и отрицательны, если направления оси OY и скоростей противоположны.
Движение тела, брошенного горизонтально с некоторой высоты.
Это движение можно разложить на два независимых движения:
§ Равномерное и прямолинейное, происходящее в горизонтальном направлении со скоростью, равной начальной скорости бросания υ 0 (υх = υ0),
§ и свободное падение с высоты, на которой находилось тело в момент бросания, со скоростью υу = ± gt.
Траектория свободно падающего тела брошенного горизонтально – это парабола (рис.1.14).
Для описания этого движения выберем прямоугольную систему координат ХОУ. Направим ось ОХ по горизонтали, ось ОУ – по вертикали Тогда, в соответствии с формулами записанными в предыдущих параграфах, можно записать четыре уравнения
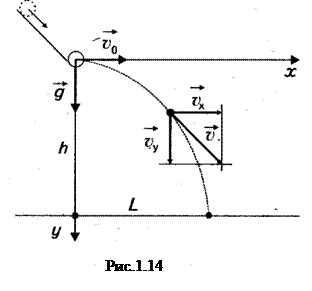 υх = υ0
υх = υ0
υу = ± gt.
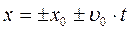
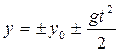
Эти четыре уравнения позволяют определить скорость и координаты (х; у) свободно падающего тела в любой момент времени
Скорость тела в любой точке траектории определяется по формуле
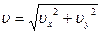
и направлена по касательной к траектории в данной точке
Дата добавления: 2015-10-09; просмотров: 2167;
