Равномерное прямолинейное движение. Графики зависимости кинематических величин от времени в равномерном движении

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость тела не изменяется ни по модулю, ни по направлению. 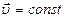, а ускорения или замедления не происходит .

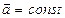Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерным прямолинейным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости.

Пройденный путь при прямолинейном движении равен модулю перемещения. Чтобы найти путь, пройденный при равномерном движении, надо скорость тела умножить на время движения:

S=υˑt

Для описания движения введём прямоугольную систему координат ХОУ. Тогда положение тела определяется его координатами Х и У.

Координаты тела определяются по формуле:

х = ±х₀ ± υ_х t

у = ±у₀ ± υ_у t

где х₀ ; у₀ – начальные координаты тела; υ_х , υ_у - проекции вектора скорости на оси координат

Значение х₀ и у₀, а также знаки перед слагаемыми в правых частях уравнений зависят от выбора начала координат и направления осей ОХ и ОУ. Если положительное направление оси ОХ совпадает с направлением движения (с направлением скорости), то проекция скорости на ось ОХ равна величине скорости и положительна. Если положительное направление оси ОХ противоположно направлению движения тела – скорость отрицательна.

Проекция перемещение на ось ОХ равна:

S=υˑt = х-х₀

График зависимости перемещения от времени показан на рис.1.5. Из графика видно, что проекция скорости равна

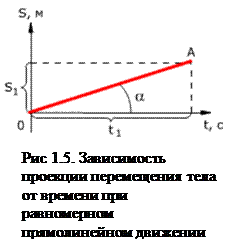
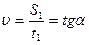
где α- угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время).

Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tgα= υ

Зависимость координаты от времени показана на рис. 1.6. Из рисунка видно, что

tgα₁> tgα₂

следовательно, скорость тела 1 выше скорости тела 2

(υ₁> υ₂)

tgα₃= υ₃˂ 0

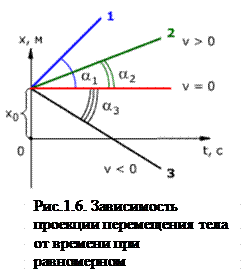Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х=х₀

Точка пересечения прямых зависимостей координаты от времени, построенных для разных тел в одном масштабе, соответствует точке встречи этих тел.

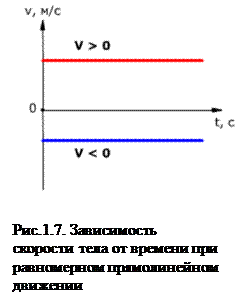График скорости равномерного движения изображен на рис.1.7. Так как скорость постоянна, то графиком скорости является прямая линия, параллельная оси времени Оt.

Площадь под графиком проекции скорости (рис.1.8) численно равна проекции перемещения, так как величина вектора 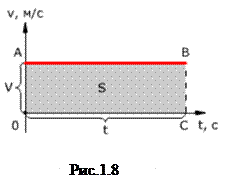перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.