Движение тела, брошенного под углом к горизонту.
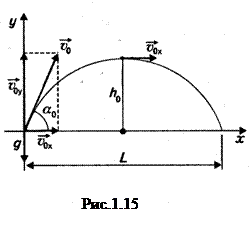
В случае, если направление начальной скорости не совпадает с направлением ускорения свободного падения, траектория движения тела, брошенного под углом к горизонту, представляет собой параболу (рис.1.15). Это движение можно разложить на два независимых движения:
· равномерное и прямолинейное, происходящее в горизонтальном направлении (направлении оси ОХ) с начальной скоростью
υ0х = υ 0 cosα ,
· и свободное падение в вертикальном направлении (направлении оси ОУ) с начальной скоростью
υ0у = υ 0 sinα
где α – угол между направлениями вектора скорости υ 0 и осью ОХ.
Зависимость горизонтальной и вертикальной координат от времени в общем виде задаётся соответственно уравнениями:
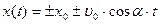
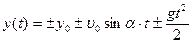
 Значение х0 и у0, а также знаки перед слагаемыми в правых частях уравнений во всех трёх случаях зависят от выбора начала координат и направления осей ОХ и ОУ.
Значение х0 и у0, а также знаки перед слагаемыми в правых частях уравнений во всех трёх случаях зависят от выбора начала координат и направления осей ОХ и ОУ.
Скорость тела в любой точке траектории определяется по формуле
|
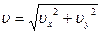
где υх = υ 0 cosα,
υу = υ 0 sinα ± gt
и направлена по касательной к траектории в данной точке.
При движении тела под углом к горизонту скорость всё время меняет своё направление. Направление вектора скорости в произвольной точке траектории определяется углом φ, образованным вектором скорости υ с осью Ох по формуле:
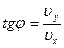
Высота, на которую тело может подняться, и дальность полёта зависит от начальной скорости и угла между горизонтом и направлением скорости (рис.1.16)
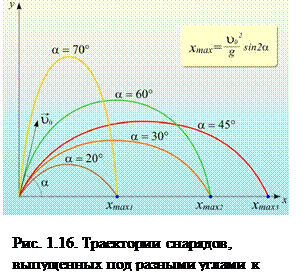 При увеличении угла бросания от 45° тело летит выше, но падает ближе. При уменьшении угла бросания от 45° тело летит ниже и ближе. Снаряды, выпущенные из пушки под углом к горизонту, летят по траекториям, называемым баллистическими. Максимальная дальность полёта достигается, если начальная скорость снаряда направлена под углом 45° к горизонту.
При увеличении угла бросания от 45° тело летит выше, но падает ближе. При уменьшении угла бросания от 45° тело летит ниже и ближе. Снаряды, выпущенные из пушки под углом к горизонту, летят по траекториям, называемым баллистическими. Максимальная дальность полёта достигается, если начальная скорость снаряда направлена под углом 45° к горизонту.
Максимальная дальность полёта тела, брошенного под углом к горизонту определяется по формуле:
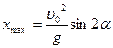
Дата добавления: 2015-10-09; просмотров: 1947;
