Показательная функция комплексного переменного
Лекция 3. Элементарные функции комплексного переменного
В комплексной области функцию требуется определить так, чтобы при  ее свойства совпадали с известными свойствами функции
ее свойства совпадали с известными свойствами функции  . Одно из важнейших свойств функции
. Одно из важнейших свойств функции  — представление ее рядом Тейлора: она является суммой сходящегося на всей числовой прямой ряда
— представление ее рядом Тейлора: она является суммой сходящегося на всей числовой прямой ряда  .
.
Учитывая это, рассматриваем ряд  и убеждаемся, что он абсолютно сходится при любом
и убеждаемся, что он абсолютно сходится при любом  , т.е. во всей комплексной плоскости
, т.е. во всей комплексной плоскости 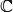 определена некоторая функция — сумма этого ряда. Так как при
определена некоторая функция — сумма этого ряда. Так как при  имеем
имеем 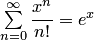 , то вводим следующее определение. Показательной функцией в комплексной области называется функция, которая является суммой сходящегося во всей комплексной плоскости ряда
, то вводим следующее определение. Показательной функцией в комплексной области называется функция, которая является суммой сходящегося во всей комплексной плоскости ряда 
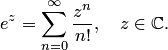 (5.1)
(5.1)
Из определения следует, что показательная функция определена во всей комплексной плоскости. В частности, при 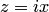 , где
, где  — действительное число, имеем
— действительное число, имеем 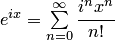 . Используя свойства абсолютно сходящихся рядов (возможность перестановки и группировки членов ряда), ряд можно записать в виде алгебраической суммы двух рядов с действительными членами отделить действительную и мнимую части ряда:
. Используя свойства абсолютно сходящихся рядов (возможность перестановки и группировки членов ряда), ряд можно записать в виде алгебраической суммы двух рядов с действительными членами отделить действительную и мнимую части ряда:

Полученные ряды являются рядами Тейлора для функций  и
и 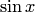 . В результате имеем равенство
. В результате имеем равенство 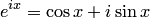 , или, обозначив
, или, обозначив  через
через 
 (5.2)
(5.2)
Формула (5.2) — формула Эйлера была использована для записи комплексного числа в показательной форме.
Функция 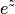 обладает, очевидно, всеми свойствами, справедливость которых установлена в действительной области, т.е. для функции
обладает, очевидно, всеми свойствами, справедливость которых установлена в действительной области, т.е. для функции  .
.
С другой стороны, в силу расширения множества, следует ожидать, что имеют место и другие свойства, аналога которых в действительной области нет.
К свойствам первой группы нужно отнести прежде всего формулу сложения:
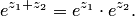 (5.3)
(5.3)
Доказательство формулы сводится, согласно определению показательной функции, к доказательству справедливости при любых 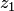 и
и 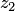 равенства
равенства  которое устанавливается путем перемножения абсолютно сходящихся рядов, записанных слева.
которое устанавливается путем перемножения абсолютно сходящихся рядов, записанных слева.
Если в равенстве (5.3) положить 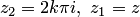 — любое комплексное число, то, учитывая тождество
— любое комплексное число, то, учитывая тождество  , можно записать
, можно записать 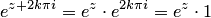 . Это равенство, справедливое при любых значениях
. Это равенство, справедливое при любых значениях  , означает, что функция
, означает, что функция 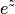 является периодической и ее наименьший период — чисто мнимое число равное
является периодической и ее наименьший период — чисто мнимое число равное 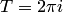 . Аналога этому свойству в действительной области нет, функция
. Аналога этому свойству в действительной области нет, функция  — непериодическая.
— непериодическая.
Так же, как и в действительной области, показательная функция 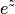 не обращается в нуль, ни при каком значении аргумента. Действительно, предположим противное. Пусть существует число
не обращается в нуль, ни при каком значении аргумента. Действительно, предположим противное. Пусть существует число 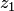 , такое при котором
, такое при котором  , тогда из тождества
, тогда из тождества  , где
, где  — любое комплексное число, получили бы,
— любое комплексное число, получили бы, 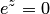 при любом
при любом  , что неверно. Однако это единственное исключение, т.е. нуль — единственное значение, которое не может принимать функция
, что неверно. Однако это единственное исключение, т.е. нуль — единственное значение, которое не может принимать функция 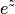 . В отличие от
. В отличие от  значение функции в комплексной области может быть отрицательным, например
значение функции в комплексной области может быть отрицательным, например  . Вообще
. Вообще 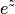 может принимать любые значения в плоскости
может принимать любые значения в плоскости 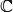 , за исключением нуля. Это свойство доказывается просто, если в формуле (5.2) положить
, за исключением нуля. Это свойство доказывается просто, если в формуле (5.2) положить  и сравнить равенство
и сравнить равенство 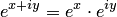 с показательной формой записи комплексного числа. В результате получим, что при фиксированном значении
с показательной формой записи комплексного числа. В результате получим, что при фиксированном значении  , модуль числа
, модуль числа 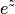 равен величине
равен величине 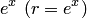 , а аргумент равен величине
, а аргумент равен величине 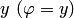 , т.е.
, т.е. 
Отсюда получаем, что 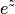 может принимать любые значения
может принимать любые значения  , так как
, так как  — любое число.
— любое число.
Пример 1. Найти  для чисел: а)
для чисел: а) 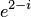 ; б)
; б)  .
.
Решение.а) Находим модуль числа 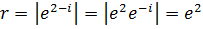 и аргумент
и аргумент  . После этого можно записать
. После этого можно записать 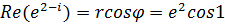 ;
; 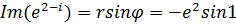 . Этот же результат можно получить другим методом
. Этот же результат можно получить другим методом 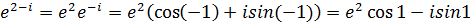 .
.
б) Представим число в виде произведения, 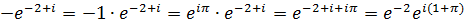 .
.
Следовательно, 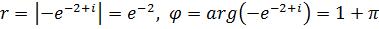 ,
, 
Пример 2. Найти  , если
, если 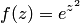 .
.
Решение.  . Следовательно,
. Следовательно, 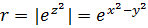 ,
, 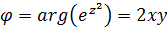 . Тогда,
. Тогда,  ,
, 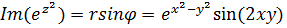 .
.
Пример 3. Показать, что функция 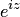 является периодической и ее период — действительное число.
является периодической и ее период — действительное число.
Решение.Нужно показать, что существует такое число 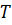 , что выполняется равенство
, что выполняется равенство 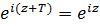 . Так как справедливо равенство
. Так как справедливо равенство 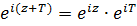 , то число
, то число 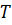 должно быть таким, что бы выполнялось равенство
должно быть таким, что бы выполнялось равенство  , а это верно при
, а это верно при  .
.
Пример 4. Доказать, что функция 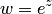 является неоднолистной на множестве
является неоднолистной на множестве 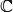 . Найти область однолистности.
. Найти область однолистности.
Решение. Пусть  , значения функции равны в этих точках
, значения функции равны в этих точках  , если
, если  . Это и означает неоднолистность функции.
. Это и означает неоднолистность функции.
Чтобы определить область однолистности запишем разность 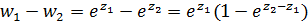 . Значения функции совпадают для тех
. Значения функции совпадают для тех 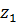 и
и  , для которых выполняется равенство
, для которых выполняется равенство 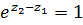 или
или 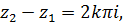 где
где 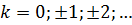 .
.
 Следовательно, однолистной функция будет в любой области, принадлежащей горизонтальной полосе ширины
Следовательно, однолистной функция будет в любой области, принадлежащей горизонтальной полосе ширины  ,
,  , в частности, в полосе
, в частности, в полосе 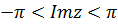 или
или  (Рис. 5.1).
(Рис. 5.1).
 | |||
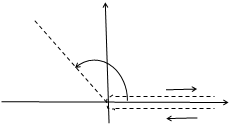 | |||









Любая прямая  (
( 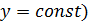 , параллельная действительной оси отображается в луч
, параллельная действительной оси отображается в луч 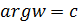 , так как из равенства
, так как из равенства 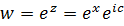 получаем
получаем  ,
, 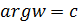 . В частности, действительная ось
. В частности, действительная ось  , то есть
, то есть  переходит в луч
переходит в луч 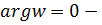 действительную положительную полуось, а прямая
действительную положительную полуось, а прямая 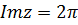 , то есть, прямая
, то есть, прямая 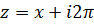 , в луч
, в луч 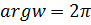 , геометрически это
, геометрически это  та же действительную положительную полуось. Для однозначности функции проведем разрез по лучу. При этом, точкам прямой
та же действительную положительную полуось. Для однозначности функции проведем разрез по лучу. При этом, точкам прямой  будут соответствовать точки нижнего берега разреза, а точкам прямой
будут соответствовать точки нижнего берега разреза, а точкам прямой  точки нижнего берега разреза
точки нижнего берега разреза
Полученный результат запишем в виде утверждения: функция 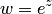 взаимно однозначно отображает:
взаимно однозначно отображает:
1) любую полосу  — в плоскость с разрезом по лучу
— в плоскость с разрезом по лучу  ;
;
2) полосу 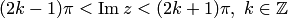 в плоскость с разрезом по действительной отрицательной полуоси;
в плоскость с разрезом по действительной отрицательной полуоси;
3) полосу  во всю комплексную плоскость с разрезом по действительной положительной полуоси.
во всю комплексную плоскость с разрезом по действительной положительной полуоси.
Дата добавления: 2015-10-09; просмотров: 2770;
