Тригонометрические и гиперболические комплексные функции
Функции 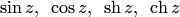 вводятся аналогично показательной функции — как суммы соответствующих абсолютно сходящихся во всей комплексной плоскости рядов:
вводятся аналогично показательной функции — как суммы соответствующих абсолютно сходящихся во всей комплексной плоскости рядов:
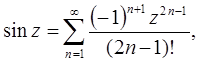
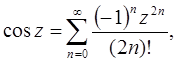 (5.4)
(5.4)
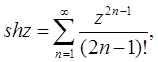
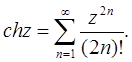 (5.5)
(5.5)
На основе этих функций определяются и другие тригонометрические и гиперболические функции:
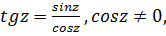
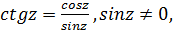
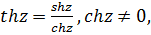
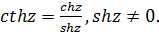
Из определений следует, что функции 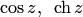 являются четными, а остальные — нечетными.
являются четными, а остальные — нечетными.
Сравнивая формулы (5.4) и (5.5) с формулой (5.1) — определением функции 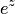 , получаем следующие формулы, справедливые при любом
, получаем следующие формулы, справедливые при любом 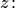
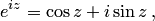 (5.6)
(5.6)
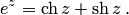 (5.7)
(5.7)
Формулы (5.6) и (5.7) — формулы Эйлера; они связывают тригонометрические и гиперболические функции с показательной. Формула (5.6) при 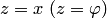 , где
, где 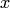 — действительная переменная, рассмотрена выше.
— действительная переменная, рассмотрена выше.
Так как формулы (5.6) и (5.7) верны при любых значениях  , то, заменяя
, то, заменяя  на
на 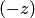 и учитывая, что
и учитывая, что 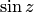 и
и 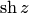 — нечетные, a
— нечетные, a 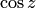 и
и 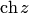 — четные функции, можем записать
— четные функции, можем записать
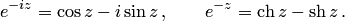
Комбинируя эти формулы с (5.6) и (5.7), получаем представление тригонометрических и гиперболических функций через показательную функцию:
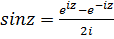 ,
, 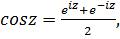 (5.8)
(5.8)
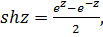
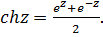 (5.9)
(5.9)
Эти формулы позволяют использовать при исследовании гиперболических и тригонометрических функций в комплексной области свойства показательной функции и не обращаться к определениям (5.4),(5.5), т.е. не рассматривать более сложные операции — действия с рядами.
Так, с помощью (5.8) и (5.9) устанавливается справедливость таких формул сложения, как
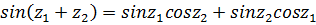 ,
,
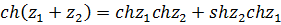 .
.
и других формул, в частности формул тригонометрии.
Кроме того, что тригонометрические и гиперболические функции выражаются через 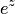 , они еще и связаны между собой. Соответствующие формулы получаются из (5.8) и (5.9)
, они еще и связаны между собой. Соответствующие формулы получаются из (5.8) и (5.9)
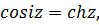
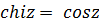 ,
, 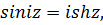
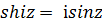 . (5.10)
. (5.10)
Отсюда, в частности, получаются такие формулы, как
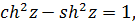
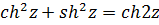
Как и в действительной области, тригонометрические функции 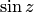 и
и 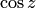 являются периодическими и их период равен
являются периодическими и их период равен 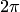 . Это следует из формул (5.8) (см. пример 3). А гиперболические функции, не будучи периодическими в действительной области, в комплексной области являются периодическими, их период, как и у функции
. Это следует из формул (5.8) (см. пример 3). А гиперболические функции, не будучи периодическими в действительной области, в комплексной области являются периодическими, их период, как и у функции 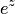 , — мнимое число
, — мнимое число 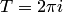 (это следует из рассмотрения равенств (5.9)).
(это следует из рассмотрения равенств (5.9)).
Замечательным свойством, не имеющим аналога в действительной области, является свойство неограниченности (по модулю) функций 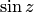 и
и 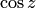 . Эти функции могут принимать любые значения, в частности большие единицы. Например, для числа
. Эти функции могут принимать любые значения, в частности большие единицы. Например, для числа 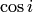 по формуле (5.8) имеем:
по формуле (5.8) имеем: 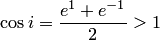 .
.
Пример 5. Найти 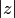 и
и 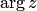 для числа
для числа 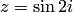 .
.
Решение.По формуле (5.10) 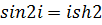 , поэтому
, поэтому 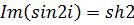 ,
, 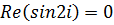 , следовательно,
, следовательно, 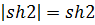 и, так как
и, так как 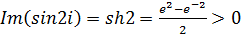 , то
, то 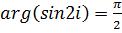 .
.
Пример 6. Найти  , если
, если 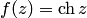 .
.
Решение. 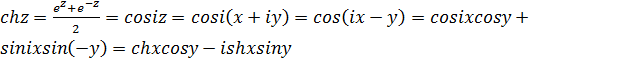 .
. 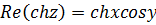 ,
, 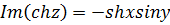 .
.
Пример 7. Найти модуль и аргумент числа 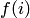 , если
, если 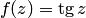 .
.
Решение. 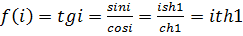 .
. 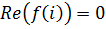 ,
, 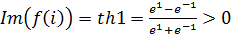 , следовательно,
, следовательно, 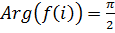 .
.
Дата добавления: 2015-10-09; просмотров: 1815;
