Обратные тригонометрические и гиперболические комплексные функции

Функции, обратные к тригонометрическим и гиперболическим функциям, определяются, как и в действительной области.

Например, обратным тригонометрическим синусом числа называется число такое, что выполняется равенство 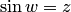. Отображение обозначается, как и в действительной области, .

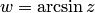Аналогично определяются и другие тригонометрические функции комплексного аргумента:

Из определений могут быть получены формулы для нахождения числа по заданному числу .

Рассмотрим эту задачу на примере нахождения 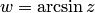. По определению имеем 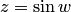. Заменим по формуле Эйлера, и из соотношения 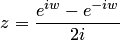или , т.е. квадратного уравнения относительно 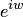, находим 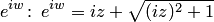. Перед радикалом записан только знак плюс, так как в комплексной области 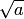— двузначное выражение. Далее, используя определение логарифма, находим

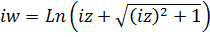и .

Для каждого числа получаем бесконечное множество значений в силу двузначности и бесконечной значности логарифма. Все это множество значений обозначается . Окончательный результат:

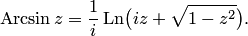(6.5)

Формулы, аналогичные (6.5), могут быть получены и для других функций:

Все эти формулы, как и (6.5), определяют многозначные функции. Выделяя однозначную ветвь выражения , можно получить однозначные функции в каждом случае.

Большого практического значения эти формулы, как и (6.5), не имеют. Для нахождения значений обратных тригонометрических и обратных гиперболических функций можно применять метод, с помощью которого выведена формула (6.5). Этим методом решен пример 6, где найдено значение .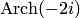

Пример 8. Решить уравнение .

Решение.Множество решений уравнения определяется уравнением 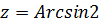или с помощью формулы (6.5) . Так как корень имеет два значения, то выражение в скобках можно записать в виде и 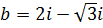. Найдем логарифмы для каждого из чисел.

а) , , поэтому

б) , , 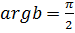поэтому 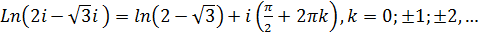. Получаем два множества решений уравнени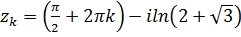й и .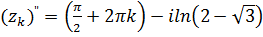

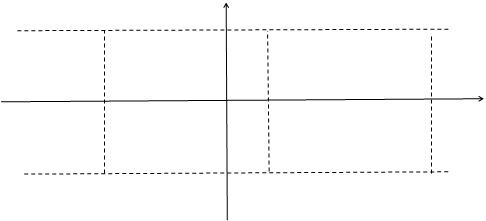
Геометрически это множество точек, расположенных на расстоянии друг от друга на прямых линиях и 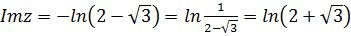, параллельных мнимой оси (рис. 6.2).

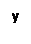
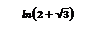
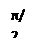
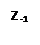
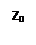
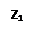
Действительных решений уравнение не имеет, так как ни при каком значении среди чисел и 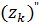нет действительных. Это соответствуют известному свойству в действительной области .