Комплексный логарифм
Понятие функции, обратной показательной функции, как и в действительной области, связано с понятием логарифма числа.
Логарифмом комплексного числа  называется число
называется число  такое, что справедливо равенство
такое, что справедливо равенство  ; обозначается
; обозначается 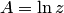 . Таким образом,
. Таким образом,  .
.
Для нахождения логарифма числа  , т.е. для нахождения действительной и мнимой частей числа
, т.е. для нахождения действительной и мнимой частей числа  , запишем число
, запишем число  в показательной форме, а число
в показательной форме, а число  будем искать в алгебраической форме:
будем искать в алгебраической форме: 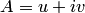 .
.
Тогда равенство 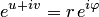 или
или 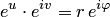 есть равенство чисел, записанных в показательной форме, и из него находим
есть равенство чисел, записанных в показательной форме, и из него находим  , то есть
, то есть 
 . Для искомого числа
. Для искомого числа  получаем выражение:
получаем выражение:
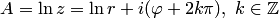 , где
, где 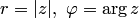 .
.
Из этого следует, что логарифм комплексного числа определяется неоднозначно; полученное выражение определяет множество значений логарифма данного числа  ; обозначается
; обозначается 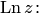
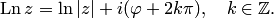 (6.1)
(6.1)
Для каждого фиксированного значения 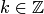 получаем определенное число — значение логарифма числа
получаем определенное число — значение логарифма числа  ; если
; если 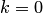 оно называется главным значением логарифма:
оно называется главным значением логарифма:
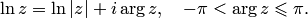 (6.2)
(6.2)
Пример 1. Найти 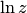 — главные значения и
— главные значения и  для следующих чисел:
для следующих чисел:
а)  ; б)
; б) 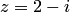 .
.
Решение. а) 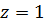 ,
,  ,
, 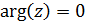 . Тогда по формуле (6.2)
. Тогда по формуле (6.2) 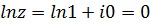 , а по формуле (6.1)
, а по формуле (6.1) 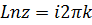 ,
,  .
.
б)  ,
,  ,
,  . Тогда по формуле (6.2)
. Тогда по формуле (6.2) 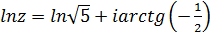 , а по формуле (6.1)
, а по формуле (6.1) 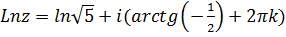 ,
,  .
.
Пример 2.Найти модуль, аргумент, действительную и мнимую части числа  .
.
Решение.Найдем модуль и аргумент числа 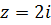 ,
, 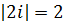 ,
, 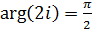 .
.
По формуле (6.2) получаем 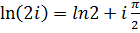 . Поэтому
. Поэтому 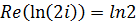 ,
,  ,
, 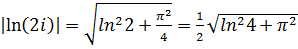 .
.
Так как 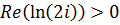 и
и  , то точка, соответствующая числу
, то точка, соответствующая числу 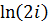 расположена в первой четверти и, следовательно,
расположена в первой четверти и, следовательно, 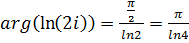 .
.
Замечание 1. Введение понятия логарифма числа позволяет определить в комплексной области степень с любым комплексным показателем 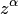 и показательную функцию с любым комплексным основанием
и показательную функцию с любым комплексным основанием  .
.
При  и
и  , где
, где 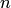 — натуральное число, степени
— натуральное число, степени  и
и 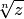 рассмотрены выше; при
рассмотрены выше; при  и
и 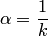 , где
, где 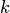 — целое число
— целое число 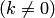 , определение к также очевидно.
, определение к также очевидно.
В общем случае при любом комплексном 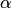 степень определяется формулой
степень определяется формулой
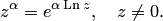 (6.3)
(6.3)
Аналогично вводится функция  с любым комплексным основанием
с любым комплексным основанием 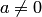
 (6.4)
(6.4)
В силу бесконечной значности логарифма, каждому числу  соответствует бесконечное множество значений степени
соответствует бесконечное множество значений степени 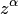 , определяемой по формуле (6.3), и бесконечное множество чисел, определяемых по формуле (6.4) при
, определяемой по формуле (6.3), и бесконечное множество чисел, определяемых по формуле (6.4) при 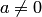 . Среди этих множеств выделяются главные значения, которые соответствуют главным значениям логарифмов.
. Среди этих множеств выделяются главные значения, которые соответствуют главным значениям логарифмов.
Пример 3. Показать, что выражение 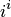 принимает только действительные значения.
принимает только действительные значения.
Решение.Используем формулу (6.4) 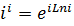 . Найдем значение
. Найдем значение  .
.
 ,
, 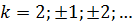 .Поэтому
.Поэтому  действительное число при любом
действительное число при любом  .
.
Пример 4. Найти  , где
, где  — корень уравнения
— корень уравнения 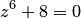 , удовлетворяющий условию
, удовлетворяющий условию  .
.
Решение.Корнем уравнения являются числа 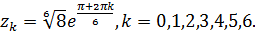 Условию
Условию  удовлетворяет
удовлетворяет 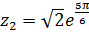 . Для найденного корня
. Для найденного корня 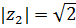 ,
, 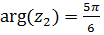 , тогда
, тогда  . Поэтому ответ
. Поэтому ответ 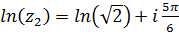 .
.
Замечание 2. Введение понятия логарифма комплексного числа позволяет решать в комплексной области показательные уравнения. Простейшим таким уравнением является уравнение вида 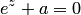 . Решение этого уравнения сводится к нахождению значений выражения
. Решение этого уравнения сводится к нахождению значений выражения 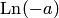 , то есть
, то есть 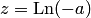 .
.
Пример 5. Решить уравнение  .
.
Решение. 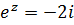 , получаем
, получаем 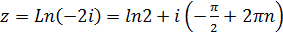 , где
, где 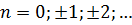 .
.
Пример 6. Найти  из уравнения
из уравнения  .
.
Решение. Используем формулу  , тогда имеем уравнение
, тогда имеем уравнение 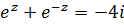 , которое сводится к квадратному уравнению
, которое сводится к квадратному уравнению  . Корни квадратного уравнения
. Корни квадратного уравнения 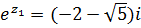 и
и 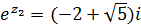 . Тогда
. Тогда 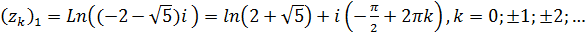 и
и 
Геометрически 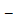 это точки, лежащие на прямых
это точки, лежащие на прямых 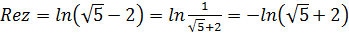 и
и  параллельных мнимой оси, расстояние между которыми равно
параллельных мнимой оси, расстояние между которыми равно  .
.
Как видим, логарифмическая функция вводится, как функция, обратная к показательной, т.е. как решение уравнения 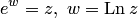 , значения функции при любом
, значения функции при любом  определяются по формуле (6.1).
определяются по формуле (6.1).
Функция, очевидно, многозначная и отображает плоскость на каждую из полос:
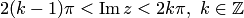 , или
, или 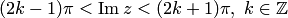 .
.
В плоскости с разрезом по лучу 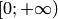 возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос 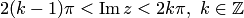 , в частности функция
, в частности функция 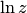 — главное значение логарифмической функции отображает плоскость на полосу
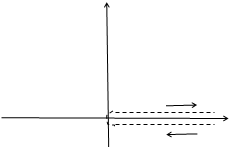
— главное значение логарифмической функции отображает плоскость на полосу  (см. рис. 6.1).
(см. рис. 6.1).
 |  | ||






В плоскости с разрезом  также возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос
также возможно выделение однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из полос 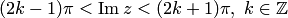 , в частности функция
, в частности функция 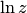 — главное значение логарифмической функции отображает плоскость на полосу
— главное значение логарифмической функции отображает плоскость на полосу 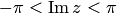 . Выделение ветви определяется заданием значения функции в одной из точек области.
. Выделение ветви определяется заданием значения функции в одной из точек области.
Пример 7. Найти решение уравнения  при условии
при условии  .
.
Решение. Так как дополнительное условие задает значение функции в точке действительной оси, то рассматривается плоскость с разрезом по действительной оси, где главное значение аргумента определяется неравенством  . Из дополнительного условия определяем значение
. Из дополнительного условия определяем значение  , соответствующее выбранной ветви
, соответствующее выбранной ветви  , следовательно, и
, следовательно, и  :
:
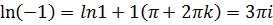 , значит,
, значит,  . Находим решение уравнения
. Находим решение уравнения  .
. 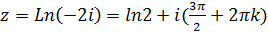 . При
. При  получаем ответ
получаем ответ 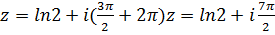 .
.
Дата добавления: 2015-10-09; просмотров: 18353;
