Риск портфеля состоящего из нескольких активов определяется по формуле
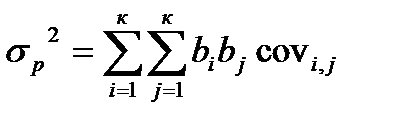
Риск портфеля, состоящего из двух активов будет определяется с учетом ковариации доходностей активов.

Пример определить риск портфеля состоящего из бумаг А и В, если bА=0,3 bВ=0,7 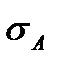 =0,0268,
=0,0268, 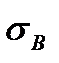 =0,02165, covAB = 0,0004562
=0,02165, covAB = 0,0004562
Тогда риск портфеля равен
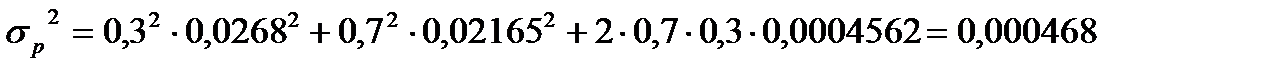
 или 2,163%
или 2,163%
Если в портфель входят два актива с корреляцией = +1, то риск портфеля определяется как средневзвешенный риск, входящих в него активов, т. к. объединение таких активов в портфель не позволяет воспользоваться возможностями диверсификации для снижения риска, т. к. доходности этих активов изм-ся в одном направлении. Следовательно, в этом случае происходит не снижение, а усреднение риска.
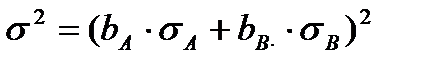

Рис. 1. Корреляции доходности +1
При корреляции = -1 происходит уменьшение риска портфеля по сравнению с риском активов, входящих в портфель. При этом ожидаемая доходность портфеля будет складываться из ожидаемых доходностей активов в них входящих с учетом их удельного веса.
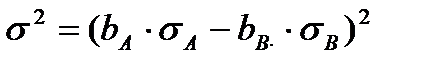
| А |
| В |
| Время |
| Доходность |
Рис. 2. Корреляции доходности -1
Сочетая активы в различных пропорциях можно сформировать портфель без риска в точке С.
| Время |
| Доходность |
| А |
| В |
| А |
| В |
| σ |
| Ep |
| С |
Рис. 3. Варианты портфеля, состоящие из двух активов с корреляцией доходности -1
Чтобы сформировать такой портфель необходимо найти соответствующие удельные веса активов А и В.

Тогда 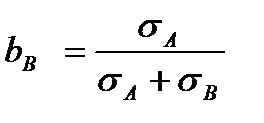 или
или 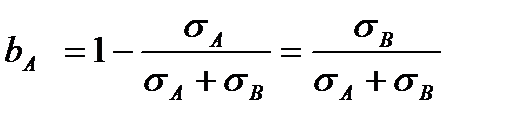
Пример 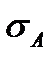 =0,0268
=0,0268 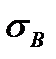 =0,0350
=0,0350
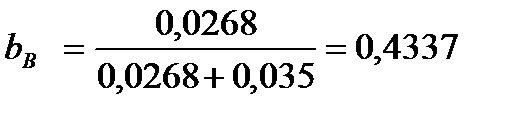
 =1-0,4337=0,5663
=1-0,4337=0,5663
Т.е. если вкладчик планирует инвестировать 100 тыс. руб. в активы А и В, то для формирования портфеля без риска ему необходимо приобрести актив А на сумму 100000*0,5663=56,63 тыс. руб. и актив В на 43,37тыс. руб.
Т. о.
1) Если корреляция активов в портфеле +1, то достигается не уменьшение, а усреднение рисков.
2) Если в портфель объединяются активы с корреляцией менее чем +1, то его риск уменьшается при сохранении доходности.
3) Чем меньше корреляция доходности, тем меньше риск портфеля.
4) Если в портфеле объединяются активы с корреляцией меньшей или равной -1, то может быть достигнут нулевой уровень риска.
| А |
| В |
| σ |
| Ep |
| С |
Корреляция между доходностями двух финансовых инструментов в портфеле может изменяться от -1 до +1.
Рис. 4. Варианты портфеля, состоящие из двух активов корреляция доходности которых изменяется -1 до +1.
На рис.4. возможные комбинации из двух активов с корреляцией -1, располагаются на прямых АС и ВС. Все комбинации портфелей для корреляции +1 – на прямой АВ. Комбинации портфелей для других значений корреляции располагаются внутри треугольника АВС.
Если построить график для портфелей, состоящих из активов АиВ при меньшей корреляции, чем +1, то он примет выпуклый вид см. рис. 5. Чем меньше корреляция между доходностями активов, тем более выпуклый будет график.
| P1 |
| А |
| В |
| σ |
| Ep |
| С |
| σ1 |
| σ2 |
| r1 |
| P2 |
Рис.6. Варианты портфелей из двух активов с различной степенью корреляции доходности
Чем меньше корреляция между активами, тем более он привлекателен для формирования портфеля, поскольку инвестор может получить тот же уровень ожидаемой доходности при меньшем риске.
Если активы имеют корреляцию меньше +1, то инвестор может сформировать любой портфель, который бы располагался на кривой ADB. Однако рациональный инвестор остановит свой выбор только на верхней части данной кривой DB.
| σ1 |
| σ3 |
| P1 |
| P2 |
| А |
| В |
| σ |
| Ep |
| D |
| P3 |
| P4 |
| r1 |
| r2 |
Рис.7 Варианты портфеля из двух активов с корреляцией доходности меньше +1
Если один портфель имеет более высокий уровень доходности при одном и том же уровне риска или более низкий риск при той же доходности, чем остальные портфели, то он называется доминирующим. Портфель P2 будет доминирующим по отношению к портфелям Р1 и Р4 нельзя сравнивать ни с каким портфелем, т.к. он имеет и наибольшую доходность и наибольший риск. Рациональный инвестор всегда сделает выбор в пользу доминирующего портфеля.
Если инвестор формирует портфель из двух активов А и В, то в точке D он получит портфель с минимальным уровнем риска. Чтобы его сформировать необходимо найти удельные веса активов А и В в портфеле. Для этого необходимо продифференцировать уравнение  и приравнять его к нулю.
и приравнять его к нулю.
Тогда 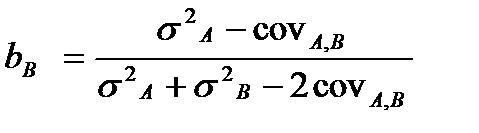 или
или 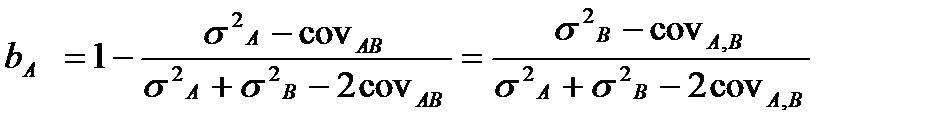
Дата добавления: 2015-10-09; просмотров: 3056;
