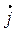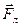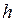Теоретическое введение. Эффект Холла (1879 г.) – это возникновение в полупроводнике (или металле) с током плотностью , помещенном в перпендикулярное току магнитное поле

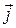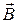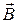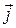Эффект Холла (1879 г.) – это возникновение в полупроводнике (или металле) с током плотностью , помещенном в перпендикулярное току магнитное поле , электрического поля в направлении, перпендикулярном и . То есть, если металлическую или полупроводниковую пластинку, по которой течет ток I, поместить в перпендикулярное току магнитное поле 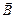, то между гранями пластинки, параллельными и полю 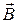, и току I, возникает Холловская разность потенциалов U_х.

Поместим полупроводниковую пластинку с током плотностью 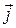в магнитное поле 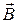, перпендикулярное 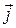(рис.15.1). Скорость 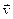носителей тока (электронов) направлена противоположно плотности тока 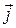. Электроны испытывают действие силы Лоренца

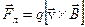, (15.1)

величина которой равна:

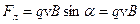, (15.1а)

так как угол α между скоростью и магнитной индукцией равен 90⁰.

Распределение зарядов в пластинке определяется по правилу левой руки. Если ладонь левой руки расположить так, чтобы вытянутые пальцы были направлены по направлению вектора плотности тока, а вектор 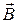входил в ладонь, то отогнутый большой палец укажет направление силы Лоренца. В данном случае сила Лоренца направлена вверх (рис.15.1).

Таким образом, на верхней грани пластинки возникнет повышенная концентрация электронов (она зарядится отрицательно), а на нижней грани – их недостаток (зарядится положительно). В результате этого между горизонтальными гранями пластинки (верхней и нижней) возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность E_B этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда F_л=F_эл, или 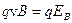. За счет возникшего поперечного электрического поля 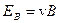между верхней и нижней гранями возникает Холловская разность потенциалов. Так как разность потенциалов и напряжённость электрического поля связаны соотношением 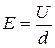, то

U_х=hE_B=hvB, (15.2)

где h – высота пластинки.

Учитывая, что плотность тока

j=qnv, (15.3)

где n – концентрация зарядов, а сила тока через образец I=jS, где S=hd – площадь сечения пластинки, получим для скорости: v=j/(qn)=I/(hdqn). С учетом (15.2) Холловская разность потенциалов:

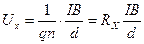, (15.4)

где

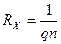(15.5)

носит название постоянной Холла. Поэтому

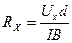, (15.6)

где I - ток через образец, d=3^.10^-4м – толщина пластинки.

По закону Ома в дифференциальной форме плотность тока j прямо пропорциональна напряженности электрического поля E:

j=gE,

где g - удельная электропроводимость. С учетом (15.3):

g=qnu, (15.7)

где u=v/E – подвижность зарядов, численно равная средней скорости направленного движения зарядов в электрическом поле с напряженностью, равной 1 В/м. Зная удельную электропроводимость образца (g=0.13(Ом^.м)^-1), полагая q=е (заряд электрона), вычислим из экспериментальных данных постоянную Холла по формуле (15.6) и рассчитаем величину подвижности:

u=g/(en)=gR_Х. (15.8)

Итак, по измеренному экспериментально значению постоянной Холла можно:

1) определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряде носителей);

2) судить о природе проводимости полупроводников, так как знак постоянной Холла совпадает со знаком заряда носителей тока.