Теоретическое введение. В пространстве, окружающем проводники с током или движущиеся заряды, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник

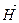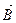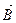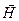В пространстве, окружающем проводники с током или движущиеся заряды, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности магнитного поля или с помощью вектора индукции магнитного поля . Векторы и связаны соотношением:

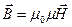, (14.1)

где 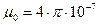Гн/м – магнитная постоянная, μ – магнитная проницаемость вещества, показывающая, во сколько раз магнитная индукция в веществе больше, чем в вакууме. Для вакуума μ=1.

Вектор напряженности 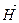характеризует только поле макротоков (проводимости или конвекционных), а вектор магнитной индукции 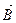– результирующее поле и макро-, и микротоков в веществе, возникших в результате намагничивания магнетика.

Для вычисления напряженности и индукции магнитного поля ис­пользуют закон Био-Савара-Лапласа, согласно которому элементар­ная напряженность магнитного поля 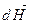, создаваемая элементом про­водника с током 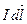в некоторой точке пространства на расстоянии 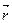, определяется выражением:

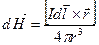. (14.2)

Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции: напряженность 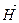магнитного поля, созданного проводником конечных размеров, равна векторной сумме элементарных напряженностей 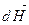магнитных полей, созданных каждым элементом тока в отдельности, то есть интегралу по контуру с током:

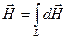. (14.3)

Применим формулы (14.2) и (14.3) для вычисления напряженности магнитного поля на оси соленоида. Каждый виток соленоида – это круговой ток, поэтому первоначально вычислим напряженность поля на оси кругового витка с током (рис. 14.1).

Элементарная напряженность 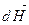поля, созданного в точке А элементом тока 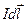, направлена по правилу буравчика перпендикулярно радиус-вектору 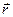, проведенному от элемента тока в точку А (рис.14.1), а ее модуль можно найти из (14.1):

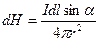, (14.4)

где α=90⁰ – угол между векторам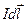и и 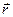. Разложим 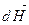на две составляющих: 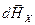– вдоль оси контура (ОХ) и 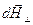– перпендикулярную оси ОХ, тогда

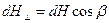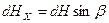, . (14.5)

При сложении составляющих магнитного поля 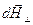, перпендикулярных оси ОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая напряженность магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:

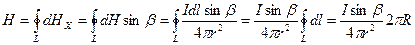(14.6)

Здесь учтено, что величины I, r, β постоянны, а интеграл по контуру 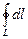равен длине окружности контура. Из рис.14.1 найдем 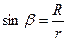, тогда:

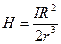, (14.7)

или:

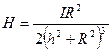. (14.8)

Перейдем теперь к вычислению поля соленоида, изображенного на рис. 14.2. Пусть на единицу длины соленоида приходится 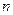витков, тогда на участке 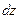будет 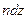витков, которые в точке О солено­ида согласно (14.7) создадут напряженность

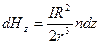(14.9)

На рис. 14.3 отдельно изображены элемент 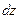, радиус-вектор 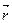и углы θ и dθ. Из геометрических построений рис. 14.2 и 14.3 следует:

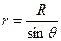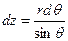, (14.10)

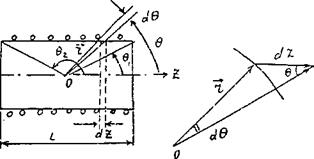
Рис. 14.2 Рис. 14.3

Подставляем (14.10) в (14.9) и интегрируем в пределах от θ₁ до θ₂:

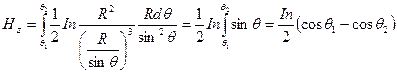(14.11)

В случае бесконечного соленоида θ₁=0, θ₂=π, и тогда

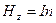. (14.12)