Лабораторна робота № 1-9 4 страница

(5)

Порядок виконання роботи

1. Закріпити на планшеті аркуш чистого паперу, рівний за величиною провідному аркушу.

2. З допомогою пантографа перенести на аркуш паперу контури електродів.

3. Скласти досліджувальну схему згідно рисунка.

4. Встановити зонд на один із електродів і за допомогою вольтметра виміряти його потенціал (у цьому випадку потенціометром R досягають відсутності струму через мікроамперметр). Аналогічну операцію проробляють і для другого електроду.

5. Змістити зонд на невелику (5-7 мм) віддаль від електрода в напрямку протилежного електрода. Потенціометром встановити нуль на мікроамперметрі. Переміщувати зонд навколо електрода таким чином, щоб покази мікроамперметра не змінювались (I=0). В процесі переміщення зонда перенести за допомогою пантографа на карту 10-15 точок першої еквіпотенціальної лінії. Еквіпотенціальна поверхня обов’язково повинна бути замкнутою. Записати рядом з нею значення потенціалу j₁. Щоб швидше і успішніше знаходити точки з однаковим потенціалом, слід керуватись міркуванням про конфігурацію досліджувального поля.

6. Змінюючи покази вольтметра кожний раз на 0,5 В, побудувати слідуючі еквіпотенціальні лінії.

Обробка результатів дослідження

1. Побудувати на одержаній карті лінії напруженості електричного поля.

2. За формулою (3) розрахувати напруженість електричного поля на кожному із відрізків еквіпотенціальної поверхні і в масштабі нанести на карту.

3. За формулою (5) розрахувати погонну ємність модельованої системи (e=1).

Контрольні запитання

1. Які основні характеристики електростатичного поля?

2. Які існують методи дослідження електростатичного поля?

3. Доведіть теорему Гаусса.

4. У чому суть явища електростатичної індукції?

5.

Лабораторна робота 2-2

Вимірювання ємності конденсаторів

л.1. §§ 26, 27.2. §§ 5.1, 5.2, 5.3

Мета роботи: набути навиків вимірювання ємності конденсаторів з допомогою місткової схеми; перевірити закони сполучення конденсаторів.

Прилади і обладнання: комплект досліджуваних конденсаторів; магазин еталонних конденсаторів; осцилограф; реохорд; з’єднувальні провідники.

Теоретичні відомості

При наданні провіднику електричного заряду його потенціал по відношенню до Землі (умовна поверхня нульового потенціалу) під­вищується. Однак відношення заряду Q до потенціалу U для даного провідника залишається постійним і називається його електричною ємністю C:

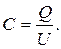(1)

При Q = 1 Кл, U = 1В знаходимо одиницю електричної ємності провідника:

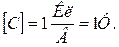
Ця одиниця називається фарадом (Ф). Фарад дорівнює електричній ємності ізольованого провідника, якщо надання йому заряду в 1Кл підвищує його потенціал на 1 В.

Електроємність залежить від геометричних розмірів і форми провідника, положення навколо нього інших провідників, електричних властивостей навколишнього середовища. Електроємність не за­лежить від матеріалу провідника і його агрегатного стану, наявності пустот і величини заряду.

Електроємність відокремленого провідника завжди мала. Збільшення електроємності за рахунок збільшення розмірів провідника не завжди виправдовує себе.

Наприклад, щоб одержати електроємність 1 мкФ, слід взяти сферичний провідник радіусом 9 км. В електро- і радіотехніці, де приходиться користуватись великими ємностями, застосовують систему провідників — конденсатори. Робота конденсаторів базується на зменшенні потенціалу зарядженого провідника під впливом іншого провідника.

Візьмемо наелектризований провідник A, заряд якого +q і внесемо в його поле інший провідник B, який в результаті явища електричної індукції електризується (рис. І). Поле наведених різнойменних зарядів послаблює наведене поле заряду +q, тому потенціал поля A падає, а електроємність зростає.

Індуковані заряди однакового знаку можна нейтралізувати, якщо заземлити провідник B. Щоб зовнішні тіла не впливали на ємність конденсатора, обкладкам надають таку форму і так розміщують їх одну відносно іншої, щоб поле, створене нагромадженими зарядами цілком було сконцентроване всередині конденсатора. Цій умові задовольняють, перш за все, поля, які створюються зарядженими площинами, коаксіальними циліндрами та концентричними сферами.

Рис. 1

Розглянемо деякі типи конденсаторів. Залежно від форми об­кладок конденсатори бувають плоскі, циліндричні, сферичні.

1) плоский конденсатор являє собою систему двох металевих, паралельних пластин (розділених діелектриком), розташованих на близькій відстані d одна від одної і однаково наелектризованих різнойменними зарядами. Знайдемо ємність такого конденсатора.

Якщо лінійні розміри пластин великі порівняно з відстанню між ними, то можна знехтувати крайовим ефектом і вважати електричне поле між пластинами однорідним:

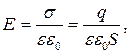(2)

інакше напруженість цього поля можна виразити через градієнт потенціалу

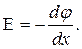(3)

З цих рівнянь дістаємо

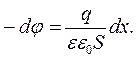
Про інтегруємо це рівняння:

,

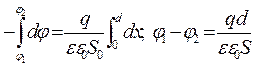звідки

.

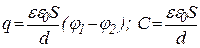Ця формула є наближеною, бо ми знехтували крайовим ефектом.

З’ясуємо вплив діелектрика на ємність конденсатора. Оскільки j₁- j₂=Ed, то формулу q = C(j₁- j₂) можна записати так:

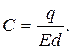
Під впливом поля E діелектрик поляризується і на його поверхнях появляються поляризаційні заряди ±s. Вектор направлений протилежно до вектора 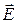, а зменшення напруженості приводить до збільшення ємності (рис.2).

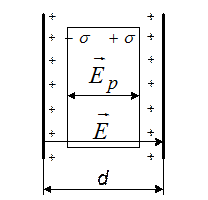
Рис. 2

2) циліндричний конденсатор являє собою систему двох порожнистих металевих коаксіальних (із спільною віссю) циліндрів, встановлених один в одного, простір між якими заповнений діелектриком (рис. 3).

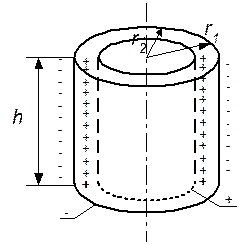
Рис. 3

Якщо висота циліндрів велика порівняно з їх радіусами (h >> r₁і r₂), то можна знехтувати крайовим ефектом і використати формулу напруженості електричного поля для нескінченно довгого зарядженого циліндра

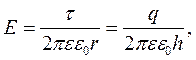
де 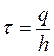— лінійна густина заряду. Напруженість можна виразити через градієнт потенціалу

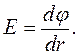
З цих рівнянь дістанемо

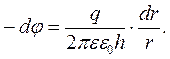
Проінтегруємо цей вираз

,

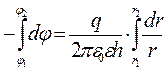Одержимо

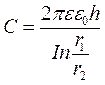(5)

Якщо зазор між обкладками конденсатора малий, тоді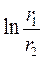
можна розкласти в ряд і обмежитися тільки членами першого поряд-
ку:

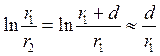
тепер

де S = 2pr₁h – бічна поверхня внутрішнього циліндра. Отже, електроємність циліндричного конденсатора можна обчислити за фор­мулою ємності плоского конденсатора;

3) сферичний конденсатор складається з двох концентричних сферичних обкладок, простір між якими заповнений діелектриком (рис. 4).

Рис. 4

Електричне поле в ньому строго радіальне. Тому сферичні конденсатори використовують в точних лабораторних дослідженнях. Потенціали обкладок такого конденсатора виражаються слідуючими співвідношеннями:

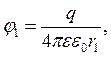
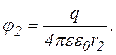
Звідки

,

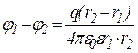або

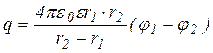
Звідки дістаємо

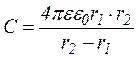(6)

Якщо r₂» r₁, тоді внутрішню обкладку можна розглядати як відокремлену кулю і формула (6) набуде такого вигляду:

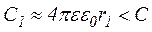
Як бачимо, електроємність конденсатора більша від електроємності відокремленого провідника. Якщо зазор між обкладками дуже малий порівняно з їх радіусами, то ємність сферичного конденсатора можна визначати за формулою плоского конденсатора, справді, при r₂- r₁ = d << r₁, r₂ » r₁ = rформула (5) набуває вигляду:

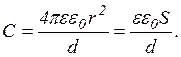
Кожний конденсатор характеризується, крім ємності, пробивною або робочою напругою. Тому для одержання необхідної ємності при заданій робочій напрузі, необхідно конденсатори з’єднувати в батареї —паралельно, послідовно або змішано.

При паралельному з’єднанні (рис.5) одна із обкладок кожного конденсатора має потенціал j₁, а друга j₂. Відповідно на кожній із двох систем обкладок нагромаджується сумарний заряд

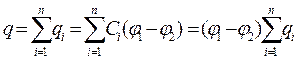
Ємність батареї одержимо, якщо розділимо сумарний заряд на при­кладену до неї напругу.

В результаті:

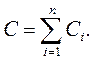(7)

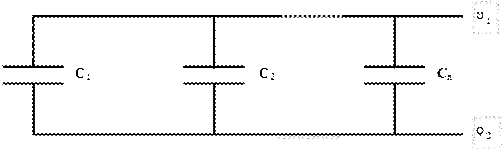
Рис. 5

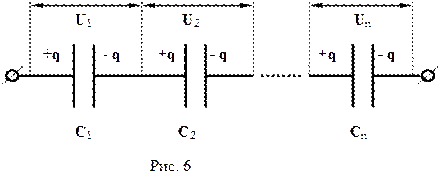
Збільшення ємності при паралельному з’єднанні конденсаторів по­яснюється тим, що збільшується робоча поверхня обкладок. Однак пробивне значення напруги батареї не перевищує пробивної напруги одного конденсатора.

При послідовному з’єднанні (рис. 6) обкладки окремих конденсаторів мають заряди, чисельно рівні, але протилежні по знаку. Тому напруга на i-му конденсаторі:

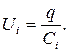
Тоді загальна напруга батареї

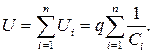
Звідки

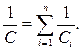(8)

При послідовному з’єднанні конденсаторів додаються величини, обернені їх ємностям, при цьому напруга на кожному конденсаторі зменшується. Якщо потрібно збільшити електроємність батареї, то, сполучають паралельно окремі групи послідовно з’єднаних конденсаторів (змішане з’єднання).

Широке поширення в лабораторній практиці при вимірюванні ємності конденсаторів одержали слідуючі методи:

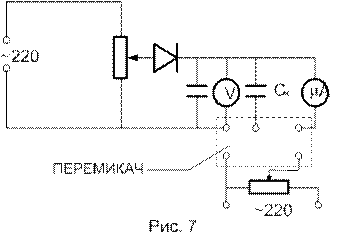
а) Періодична зарядка і розрядка. Досліджуваний конденсатор С (рис.7) заряджається через випрямляч до U. Автоматично діючий перемикач від’єднує одну із обкладок від джерела напруги і замикає обкладки конденсатора на мікроамперметр. При цьому конденсатор розряджається. Цикл зарядка-розрядка повторюється з частотою роботи перемикача ¦ = 50 Гц.

Середній заряд, який протікає через мікроамперметр за час t,

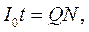
де I₀ –середня величина струму, що фіксується мікроамперметром;

Q – заряд конденсатора;

N – число розрядів за час t.

Інакше 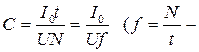частота перемикання).

б) Балістичний гальванометр. Балістичним гальванометром називають такий гальванометр, в якому момент інерції рухомої частини (котушки) спеціально збільшений. Кут відхилення котушки такого гальванометра пропорційний величині заряду, який проходить через гальванометр:

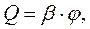
де b–балістична постійна гальванометра, яка чисельно рівна величині заряду, необхідному для повороту рамки гальвано­метра на 1 одиницю кута.

Ємність конденсатора, зарядженого до відомої різниці потенціалів U, можна визначити, розряджаючи його на гальванометр:

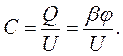
Принципіальна схема установки подана на рис. 8:

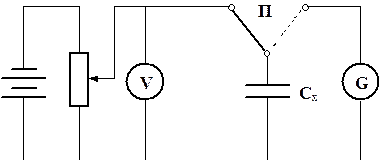
Рис. 8

в) Куметра, принцип дії якого базується на тому, що вимірювана ємність входить до складу коливального контура з малим затуханням. Ємність конденсатора можна визначити, якщо добитися резонансу в контурі, ємностний опір якого 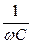дорівнює індуктивному опору 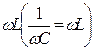. Резонансу можна добитися, змінюючи або індуктивність L , або частоту змінного струму w.

Якщо паралельно вимірювальному конденсатору С_х (рис.9) підключити проградуйований конденсатор Сзмінної ємності, то добившись резонансу 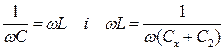(С₁ і С₂–ємності, взяті із шкали проградуйованого конденсатора), одержують: С_х=С₁ - С₂. Резонанс можна зафіксувати з допомогою покажчика лампового вольтметра (ЛВ).

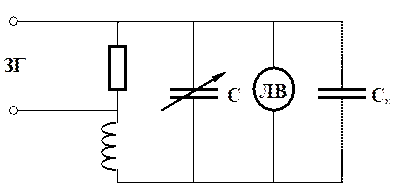
Рис. 9

г) Містковий, який знайшов найбільш широке застосування. Найбільш зручна схема містка, яка називається містком Сотті, зображена на рис. 10:

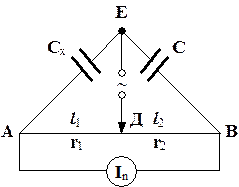
Рис. 10

За допомогою повзунка реохорда можна добитися такого положення, при якому струм, що проходить через індикатор нуля, буде відсутній (j_а=j_в)

Умова рівновагу містка виводиться таким чином : За часdtпо вітці ДАЕ пройде величина заряду:

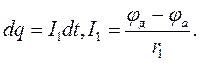
Із визначення ємності конденсатора слідує, що

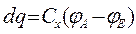
Тому,

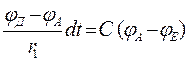
Для вітки ДЕВ по аналогії:

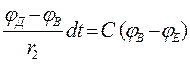
Враховуючи, що j_а=j_в,знаходимо

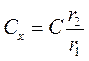
або враховуючи, що r₁ і r₂ – опори плечей реохорда, вони в свою чергу пропорційні l₁ і l₂, то

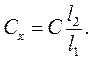(9)

При роботі з містком слід мати на увазі, що одержане рівняння справедливе для ідеальної схеми. В реальній схемі завжди є паразитні ємності і індуктивності, які тут не враховуються.

Порядок виконання роботи

1. Зібрати схему, подану на рис. 10. У ролі індикатора нуля можна використати будь-який, наявний в лабораторії осцилограф.

2. Ввімкнути в мережу 220 В осцилограф і низьковольтний трансформатор, який постачає струм в коло.

3. За допомогою повзунка Ддобитися відношення 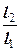, при якому довжина світлової лінії на екрані осцилографа буде найменшою. При цьому слід пам’ятати, що найбільш вигідно працювати в режимі, коли опори плеч мало відрізняються один від одного.

4. Провести вимірювання ємностей всіх наявних конденсаторів C₁,С₂,… ,С_Х.

5. З’єднати конденсатори паралельно і виміряти сумарну їх ємність.

6. З’єднати конденсатори послідовно і виміряти сумарну їх ємність.

7. Скласти таблицю, в яку занести всі виміряні і розраховані величини .

Обробка результатів вимірювання і їх аналіз

1. За формулою (9) розрахувати ємності всіх досліджуваних конденсаторів, а також паралельного і послідовного їх сполучення.

2. Перевірити закони сполучення конденсаторів теоретичними роз­рахунками і зробити необхідні висновки.

3. Провести розрахунки похибок вимірювань.

Контрольні запитання

1. Що таке електроємність провідника та від чого вона залежить?

2. Як одержати формули ємностей плоского, циліндричного і сферичного конденсаторів?

3. Як розраховують ємність батареї паралельно чи послідовно з’єднаних конденсаторів?

4. Якими методами міряють емність конденсаторів?

5. Як працює місток Сотті?

Лабораторна робота № 2-3

Визначення відносної діелектричної проникності

сегнетоелектриків.

л.1. §23. 2. §§ 6.4, 6.5

Мета роботи: вивчення властивостей сегнетоелектриків та визначення відносної діелектричної проникності титанату барію.

Прилади та матеріали: міст змінного струму Р-577 для вимірювання ємностей в межах 1 пФ-1100 мкФ і штанген­циркуль ; досліджувані сегнетоелектрики.

Теоретичні відомості

Згідно з уявленнями класичної фізики, діелектрики відрізняються від провідників тим, що при не дуже високих температурах та при відсутності дуже сильних електричних полів в них немає вільних електричних зарядів. При внесенні діелектриків в електричне поле вони поляризуються, на їх поверхні виникають зв’язані заряди і відповідне електричне поле, яке зменшує дію зовнішнього електричного поля. Для кількісної оцінки явища поляризації діелектрика користуються поняттям вектора поляризації Р , що характеризується електричним дипольним моментом одиниці об’єму діелектрика:

,

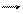
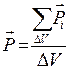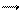деР_i – дипольні моменти окремих молекул, які знаходяться в об’єміDV;

DV – фізично безмежно малий об’єм.

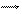Для широкого класу ізотропних діелектриків та широкого кола явищ вектор поляризації пропорційний вектору напруженості електричного поля всередині діелектрика E :

,

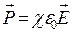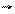де c – діелектрична сприйнятливість речовини діелектрика (величина безрозмірна). Такий характер залежності між Р і E пояснюється тим, що напруженість макроскопічних електричних полів здебільшого значно менша напруженості мікрополів в середині атомів та молекул.

Електричним зміщенням називають векторну величину

.

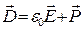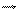
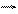В ізотропних діелектриках D і Eзв’язані співвідношенням:

,

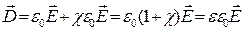де e – відносна діелектрична проникність речовини.

З молекулярної точки зору поляризація діелектриків полягає або в зміщенні пружно зв’язаних зарядів, що входять до складу молекули, атома чи іона, в електричному полі (пружна поляризація), або в виникненні дипольних молекул та іонів під дією електричного поля (релаксаційна поляризація). Пружна поляризація може бути електронною чи іонною.

Якщо діелектрик складається з неполярних молекул, то в електричному полі відбувається зміщення електронів відносно ядер в атомах чи іонах і молекули набувають дипольного моменту (індукційний дипольний момент), який пропорційний напруженості електричного поля E . Таким чином, cта e для цих діелектриків не залежать від E . Характерною особливістю електронної поляризації являється незалежність c таe від температури.

Іонна поляризація пружного зміщення виникає при зміщенні в електричному полі позитивних та негативних іонів, які створюють решітку іонних кристалів, від їх положень рівноваги. І в цьому випадку також зв’язок між Р та E лінійний, тобто e не залежать від E .

Існують діелектрики, молекули яких у відсутності електричного поля мають власні дипольні моменти (полярні молекули). При E=0 такий діелектрик не поляризований, тому що завдяки теплового руху молекули-диполі хаотично зорієнтовані в просторі. Зовнішнє електричне поле приводить до орієнтації диполів вздовж силових ліній і діелектрик поляризується. Поляризація діелектрика в основному викликана орієнтацією молекул, тому що одночасно в електричному полі у молекул виникає індукційний дипольний момент, значно менший власного дипольного моменту полярних молекул. Орієнтації молекул заважає їх тепловий рух. Якщо електричне поле забрати, то поляризація зникає, або релаксує,— звідси й назва — релаксаційна (теплова) поляризація, у випадку орієнтаційної поляризації вектор Р лінійно зростає із збільшенням на-пруженності поля E. Але при цьому діелектрична сприйнятливість c, а також відповідно проникність e значно залежать від температури, зменшуючись з її підвищенням.

Відомі діелектричні кристали з незвичайними електричними вла­стивостями. Навіть при відсутності електричного поля решітка додатних іонів в стані термодинамічної рівноваги у них зміщена відносно решітки від’ємних іонів, тому кристал виявляється поляризованим. Така самостійна поляризація називається спонтанною, а кристали - піроелектричними. Характерним прикладом піроелектричних кристалів являється турмалін.

Існує клас кристалічних діелектриків, які в певній області температур, яка носить назву полярної області, являються піроелектриками. На границях полярних областей у таких діелектриків відбуваються фазові переходи із зміною кристалічної модифікації, що супроводжується зникненням спонтанної поляризації. Такі діелектрики називаються сегнетоелектриками, так як вперше ці властивості були виявлені у сегнетової солі. По аналогії з феромагнетиками верхня межа полярної області називається точкою Кюрі Т_К , а нижня межа може бути відсутня.

Ще однією характерною рисою сегнетоелектриків являється те, що напрямок їх спонтанної поляризації може бути легко замінений на протилежний навіть в слабкому електричному полі. У звичайних піроелектриків така заміна напрямку спонтанної поляризації не може бути досягнута навіть у сильних полях.

Пряма, що паралельна векторові спонтанної поляризації сегне­тоелектрика, називається його полярною віссю. Сегнетоелектрики можуть мати одну полярну вісь, наприклад, сегнетова сіль, або кілька полярних осей, наприклад, титанат барію ВаТіО₃.

Так як сегнетоелектрикам в полярній області температур властива спонтанна поляризація, то це означає, що такий стан більш стійкий, ніж неполярний, тобто відповідає мінімальній повній енергії сегнетоелектрика. Це можливе тільки тоді, коли при відсутності зовнішнього електричного поля в об’ємі досить великого сегнетоелектрика будуть утворюватись області з різним напрямком вектора поляризації - домени. Утворення доменів приводить до зменшення повної енергії сегнетоелектрика. Дійсно, повна енергія сегнетоелектрика складається з енергії всіх доменів, енергії зовнішнього електричного поля та поверхневої енергії на границях розділу доменів. Енергія зовнішнього електричного поля найбільша тоді, коли сегнетоелектрик має однаковий напрямок вектора поляризації в усьому об’ємі. Ділення на домени зменшує енергію зовнішнього поля, одночасно збільшуючи поверхневу енергію на границях доменів. Процес розпаду сегнетоелектриків на домени припиняється, коли внаслідок наявності двох конкуруючих процесів повна енергія кристалу стане мінімальною.

Завдяки доменній структурі дипольний момент сегнетоелектрика при відсутності зовнішнього електричного поля дорівнює нулеві, так як напрямок спонтанної поляризації доменів різний. В такому розумінні цей сегнетоелектрик є неполяризованим. Якщо сегнетоелектричний зразок внести в електричне поле, в ньому від­буватиметься переорієнтація доменів та ріст одних за рахунок інших. Це приводить до поляризації кристалу. Але у сегнетоелектриків вектор поляризації Р залежить від Е нелінійно. Запи­суючи співвідношення Р=e₀cЕ, слід пам’ятати, що cне є сталою величиною, а є функцією від Е . При цьому для сегнетоелектриків в полярній області може досягати аномально великих значень порядку 10⁴ і навіть більше.

Сегнетоелектрики знаходять широке практичне застосування в сучасній електро- та радіотехніці, їх використовують для виготовлення конденсаторів малих розмірів, генерування та прийому ультразвукових хвиль, модуляції частоти електромагнітних коливань і т.д.

Порядок виконання роботи

1. Штангенциркулем заміряти параметри пластин сегнетоелектриків і для кожного з них вирахувати площу S.

2. Розташувати сегнетоелектрик між пластинами плоского конденсатора і з допомогою мосту змінного струму Р-577 заміряти його електричну ємність.

3. Результати вимірювань та обчислень для кожного сегнетоелектрика занести в таблицю.

Обробка результатів експерименту

1. Вирахувати відносну діелектричну проникність кожного сег­нетоелектрика, використовуючи формулу ємності плоского конденсатора

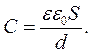
2. Вирахувати абсолютну та відносну похибки вимірювань.

3. Результати роботи проаналізувати та зробити висновки.

Контрольні запитання

1. Різниця між діелектриками і провідниками.

2. В чому полягає поляризація діелектриків? Що таке вектор поляризації?

3. Які види поляризації ви знаєте? Охарактеризуйте їх.

4. Розкажіть про головні особливості сегнетоелектриків та про їх застосування.

Лабораторна робота № 2-4

Дослідження температурної залежності

властивостей сегнетоелектриків та визначення точки Кюрі

л. 1. § 23. 2. §§ 6.4, 6.5

Мета роботи: вивчення залежності електричних властивостей сегне­тоелектриків від температури і визначення точки Кюрі.

Прилади і матеріали: експериментальна установка; досліджуваний сегнетоелектрик.

Теоретичні відомості

Основні електричні властивості діелектриків, піроелектриків і сегнетоелектриків розглянуті в попередній лабораторній роботі (2-3). У даній роботі досліджується температурна залежність діелектричної проникності сегнетоелектриків, так як вона грає важливу роль при їх технічному застосуванні.