Лабораторна робота № 2-6 4 страница
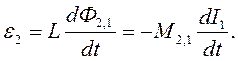 (2)
(2)
Формула (2) справедлива при відсутності феромагнетиків.
Якщо поміняти місцями контури 1 і 2 і провести всі попередні міркування, то одержимо
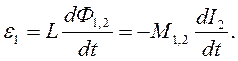 (3)
(3)
Можна показати, що коефіцієнт взаємної індукції
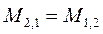 (4)
(4)
У даній роботі вимірюється коефіцієнт взаємної індукції між довгою котушкою 1 і короткою 2, яка одягається на котушку 1 і може переміщуватись вздовж її осі. Живлення однієї із котушок, наприклад 1, здійснюється від генератора звукової частоти ЗГ, напруга якого
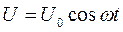 (5)
(5)
подається через опір R. Вольтметр, розміщений на панелі вимірює діюче значення напруги 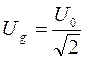 . R вибирається таким чином, щоб виконувалась нерівність
. R вибирається таким чином, щоб виконувалась нерівність
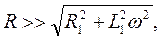 (6)
(6)
де L1– індуктивність котушки 1;
R1 – її активний опір.
У цьому випадку струм, який протікає через котушку 1,створює змінну ЕРС взаємної індукції в котушці 2:
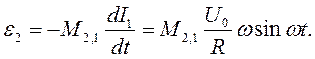 (7)
(7)
Змінний струм у котушці 2 створює змінну ЕРС взаємної індукції в котушці 1:
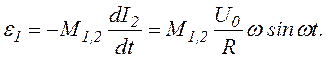 (8)
(8)
Для вимірювання e2 використовується осцилограф. Амплітуда ЕРС взаємної індукції:
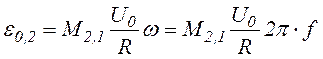 (9)
(9)
де ¦– частота звукового генератора.
Із співвідношення (9) маємо
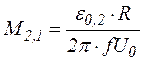 (10)
(10)
Якщо поміняти місцями котушки 1 і 2, то можна виміряти
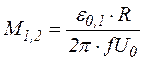 (11)
(11)
Для перестановки котушок слід перемикачі П1і П2 перекинути в протилежні положення (рис.2 ).
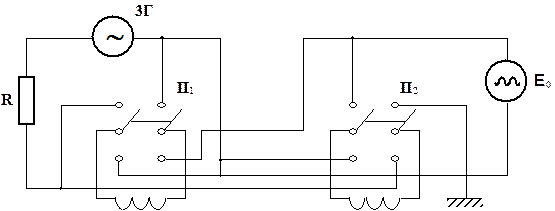
Рис. 2.
Порядок виконання роботи.
Завдання 1. Вимірювання коефіцієнтів взаємної індукції M2,1 і M1,2 і дослідження їх залежності від взаємного розміщення котушок.
1. Зібрати схему, зображену на рис. 2 і 3 .
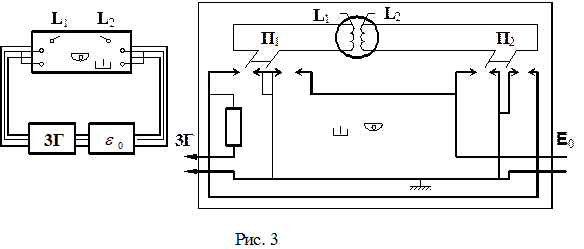
2. Ознайомитись з роботою електронного осцилографа і звукового генератора.
3. Задати напругу Uq і частоту ¦сигналу генератора (за вказівкою викладача), подати напругу на котушку 1 (за допомогою перемикача П1), а ЕРС котушки 2 на осцилограф (за допомогою вимикача П2)
4. Встановити рухому котушку 1 в крайнє положення. Переміщуючи її в протилежне крайнє положення через 1 см, записати значення е.р.c. взаємної індукції в колі котушки 2.
5. За формулою (10) розрахувати значенняM2,1. Одержані значення виміряних величин занести до таб. 1.
6. Поміняти місцями котушки L1 i L2 за допомогою перемикачів П1 і П2, повторити вимірювання згідно пунктів 2 і 3 і розрахувати М1,2.
7. Побудувати графіки залежності M2,1 і М1,2 як функції координати Z (Z- віддаль між центрами котушок 1 і 2).
Таблиця 1.
| U= | ¦= | ||||||
| Z,см | e0,2 | М2,1, Гн | e0,1 | М1,2,Гн | |||
| поділ. | В | поділ. | В | ||||
Завдання 2. Вимірювання М2,1при різних значеннях амплітудного значення напруги генератора.
1. Помістити котушку 1 в середнє положення відносно котушки 2.
2. Установити частоту генератора за вказівкою викладача (наприклад, 104 Гц).
Виміряти амплітуду ЕРС взаємної індукції при різних значеннях напруги в колі котушки 1 в інтервалі О-5 В через 0,1 В.
5. За формулою (10) розрахуватиМ2,1. Одержані значення вимірювальних величин занести до таб. 2.
Таблиця 2.
| ¦= | R=104Ом | ||||
| Uq, B | |||||
| М2,1, Гн | |||||
| e0.2, В |
Завдання 3. Вимірювання М2,1при різних частотах напруги живлення.
1. Помістити котушку 1 в середнє положення відносно котушки 2.
2. Установити амплітуду живлення генератора (за вказівкою викладача), наприклад, 2В.
3. Виміряти амплітуду ЕРС взаємної індукції E02 при різних частотах звукового генератора від 5 до 20 кГц (одержати біля 10 вимірювань).
4. За формулою (10) розрахуватиМ2,1. Одержані значення занести до таб.3.
Таблиця 3.
| UB= | R=104 Ом | ||||
| ¦, Гц | |||||
| М2,1 , Гн | |||||
| e0.2, В |
5. Для одного із одержаних значеньМ2,1розрахувати абсолютну і відносну похибки.
Контрольні запитання
1. Сформулювати закон електромагнітної індукції Фарадея і правило Лєнца.
2. Суть явища взаємної індукції.
3. Чому дорівнює е.р.с. взаємної індукції двох контурів?
4. Пояснити графік залежності М2,1 =¦(Z), одержаний у цій роботі.
Лабораторна робота № 3-7
Визначення відносної магнетної проникності магнетиків з допомогою містка Максвелла
л.І. §§51,52,53. 2 .§§20.1,20.5
Мета роботи: засвоєння навичок визначення відносної магнітної проникності різних феромагнетиків з допомогою містка Максвелла.
Прилади та матеріали: індикатор нуля; еталонна катушка індуктивності; реохорд; три тороїди з досліджуваними магнетиками; трансформатор.
Теоретичні відомості
Атоми та молекули матеріальних тіл є складними системами рухомих електричних зарядів, які можна розглядати як мікроскопічні “молекулярні струми”, кожний з яких має магнетний момент і створює магнетне поле. Якщо результуючий магнетний момент всіх електронів атома чи молекули даної речовини виявляється рівним нулеві, то ця речовина - діамагнетик, а якщо відмінним від нуля, то- парамагнетик.
У зовнішньому магнітному полі під дією сили Лоренца відбувається відповідна зміна в обертовому русі електронів, що приводить до виникнення у всіх без винятку атомах і молекулах наведених магнетних моментів, спрямованих за законом Лєнца завжди проти поля. Це явище носить назву діамагнітного ефекту. Таким чином, намагнечування діамагнетиків зводиться до появи у частинок лише наведених магнетних моментів, що приводить до ослаблення зовнішнього магнетного поля в діамагнітних речовинах.
При внесенні в магнетне поле парамагнетиків власні магнетні моменти атомів і молекул, які до цього мали зовсім хаотичний напрямок, частково орієнтуються в напрямку намагнечуючого поля. Це приводить до підсилення результуючого магнетного поля в парамагнетних речовинах. Розмагнічуюча дія наведених моментів спостерігається також і тут, але вона порівняно невелика.
Індукцію магнетного поля всередині речовини можна розглядати як суму:
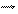
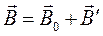 (1)
(1)
де В0 – індукція зовнішнього намагнечуючого поля;
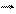 В¢ –індукція власного внутрішнього поля речовини.
В¢ –індукція власного внутрішнього поля речовини.
Ступінь намагнечування речовини визначають вектором намагнеченості, що дорівнює векторній сумі магнетних моментів всіх частинок речовини в одиниці об’єму:
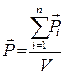 (2)
(2)
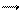 У діа- і парамагнетиків вектор намагнеченості прямо пропорційний напруженості магнетного поля Н0:
У діа- і парамагнетиків вектор намагнеченості прямо пропорційний напруженості магнетного поля Н0:
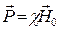 (3)
(3)
Коефіцієнт пропорційності c називається магнетною сприйнятливістю речовини.
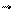

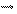 Вектори індукції В0 та В¢ зв’язані з Н0 та Ртакими співвідношеннями:
Вектори індукції В0 та В¢ зв’язані з Н0 та Ртакими співвідношеннями:
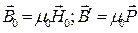 (4)
(4)
де 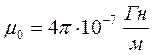 — магнетна стала в системі СІ.
— магнетна стала в системі СІ.
З врахуванням (3) та (4) векторна сума (1) приймає вигляд:
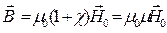 (5)
(5)
Величину m=1+cназивають відносною магнітною проникністю речовини.
 Для діамагнетиків m<1 ; c<0,а для парамагнетиків m>1 ; c>0і вони для цих речовин від напруженості зовнішнього намагнічуючого поля Н0 практично не залежать. У речовин цих груп відносна магнетна проникність мало відрізняється від одиниці, а магнетна сприйнятливість — від нуля, тобто, m»1; c»0
Для діамагнетиків m<1 ; c<0,а для парамагнетиків m>1 ; c>0і вони для цих речовин від напруженості зовнішнього намагнічуючого поля Н0 практично не залежать. У речовин цих груп відносна магнетна проникність мало відрізняється від одиниці, а магнетна сприйнятливість — від нуля, тобто, m»1; c»0
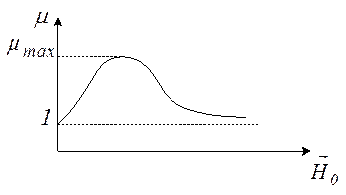
Серед парамагнетиків виділяється особлива група сильно магнетних речовин - феромагнетиків (залізо, кобальт, нікель, їх сплави), які характеризуються дуже великою відносною магнетною проникністю (наприклад, для чистого заліза mmax=2,8×105), a також її залежністю від напруженості намагнечуючого поля та наявністю залишкової намагнеченості.
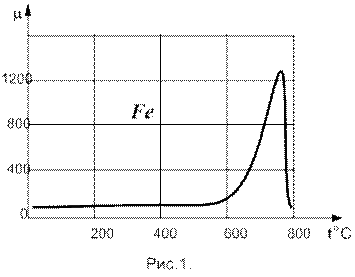
Високі магнетні якості феромагнетиків обумовлені колективними властивостями великих груп атомів створювати області (домени) спонтанної намагнеченості до насичення. Без поля полікристалічний зразок не проявляє намагнеченості, так як магнетні проявляє намагнеченості, так як магнітні моменти сусідніх доменів орієнтовані хаотично. В магнетному полі відбувається орієнтація магнетних моментів доменів в напрямку магнетних силових ліній. Але залежність індукції магнітного поля феромагнетика B від напруженості намагнечуючого поля не являється лінійною, так як магнітна проникність феромагнетиків m в свою чергу залежить від H0 (див. рис.1).
Відомо, що індуктивність тороїда визначається за формулою:
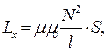 (6)
(6)
де N – повне число витків;
l – довжина середньої лінії тороїда ;
S– площа поперечного перерізу тороїда, обмежена його витками.
 Як бачимо, в формулі (6) тільки m залежить від H0 , решта всі величини сталі. Таким чином, якщо відома індуктивність тороїда Lxі його характеристики N, l, S, то можна визначити m .
Як бачимо, в формулі (6) тільки m залежить від H0 , решта всі величини сталі. Таким чином, якщо відома індуктивність тороїда Lxі його характеристики N, l, S, то можна визначити m .
Значення індуктивності Lx в роботі визначається з допомогою містка Максвелла, схема якого зображена на рис.2, де Lx і Rx—відповідно індуктивність і омічний опір тороїда, осердя якого виготовлене з досліджуваного феромагнетика; L, R – відповідно індуктивність і омічний опір еталонної котушки;IH – індикатор нуля, АВ– реохорд;l1, l2 – плечі реохорда.
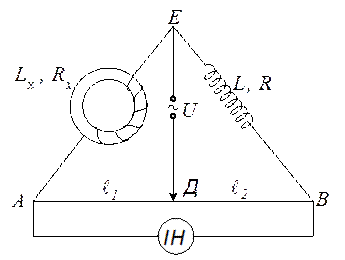
Пересуваючи повзунок реохорда D, можна добитися такого положення, при якому струм через індикатор нуля відсутній. При цьому jA= jB, тоді можна записати:
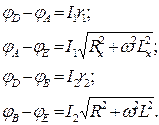
Розв’язуючи одержану системурівнянь при умові, що jA= jBодержуємо:
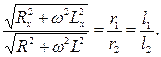
Тут r1і r2опори дільниць AD i DB реохорда, відношення яких правомірно замінено відношенням їх довжин. З останнього співвідношення знаходимо індуктивність тороїда:
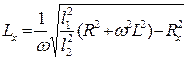 , (7)
, (7)
значення якої треба підставити в формулу (6) для знаходження відносної магнітної проникності досліджуваного матеріалу осердя тороїда.
Порядок виконання роботи
1. Зібрати схему (рис.2) і, після перевірки лаборантом, ввімкнути в мережу.
2. З’єднати з вимірювальною схемою містка Максвелла кінці першого тороїда і пересуваючи повзунок D реохорда добитися мінімальних розмірів індикаторної риски на IH
3. Записати значення плеч реохордаl1il2.
4. Перемикачем змінити величину напруги U і заміряти нові значення l1 i l2.
5. Проробити вимірювання за пп. 2- 4 для другого і третього тороїдів.
Обробка результатів експерименту і їх аналіз
1. Взявши значення L, R, Rx,які вказані на відповідних елементах схеми, і враховуючи, що w= 2pn (n=50 Гц) за формулою (7) вирахувати по два значення Lx для кожного тороїда.
2. Вирахувати за формулою (6) по два значення m для кожного осердя. Число витків кожного тороїда N дається, а довжину середньої лінії lплощу перерізу S вирахувати за вказаними геометричними розмірами.
3. Зробити аналіз одержаних результатів, пояснити відмінність значень mдля одного осердя.
4. Обчислити абсолютну і відносну похибки для будь-якого значення m.
Контрольні запитання
1. Які явища відбуваються в речовині при її внесенні в магнетне поле?
2. Дайте визначення вектора намагніченості та як він зв’язаний з індукцією магнетного поля.
3. Поясніть фізичний зміст магнітної проникності речовини і її залежність від температури.
4. Які особливості магнетних властивостей феромагнетиків? Охарактеризуйте криву намагнечування.
5. Поясніть суть явища гістерезису.
Лабораторна робота №3- 8
Дослідження кривих намагнечування та петель гістерезису феромагнетиків з допомогою осцилографа
л.1. §§53, 59.2 §§20.5, 20.6, 20.7
Мета роботи: зняття кривих намагнечування різних феромагнетиків та вивчення особливостей їх петель гістерезису.
Прилади та матеріали: набір феромагнетних зразків з намотаними на них намагнечувальними та індикаторними котушками; осцилограф; реостат; конденсатор.
Теоретичні відомості
Особливий клас магнетиків складають феромагнетики, для яких характерна наявність областей спонтанного намагнічування, які називаються доменами. У межах кожного домену феромагнетик спонтанно намагнечений до насичення і має певний магнетний момент. Напрямки цих моментів для різних доменів різні, тому при відсутності зовнішнього магнетного поля результуючий момент всього тіла дорівнює нулеві. Розміри доменів складають біля кількох мікрометрів.
Попадаючи в магнетне поле, навіть відносно слабке, магнетні моменти доменів орієнтуються вздовж силових ліній і зразок намагнечується. Намагнеченість феромагнетиків незрівнянно більша (до 107 разів) від намагнеченості діа- і парамагнетиків.
Феромагнетикам властива важлива особливість, яка подібна до запам’ятовування, тобто стан феромагнетика залежить не тільки від напруженості магнетного поля в даний момент, але й від того, які зміни в магнетному полі були раніше.
Тому в загальному випадку індукція магнетного поля В феромагнетика є складною функцією напруженості поля Н .

 Розглянемо цю залежність. Якщо повністю розмагнечений феромагнітний зразок внести в магнетне поле то при рівномірному збільшенні напруженості магнетного поля залежність В від Н зображається дільницею оа (рис.1), яка носить назву основної кривої намагнечування. При подальшому збільшенні напруженості поля Н ця крива переходить в лінійну залежність, так як намагнеченість досягає насичення і залишається сталою, а В зростає тільки за рахунок збільшення Н, при зменшенні Н до нуля крива розмагнечування не співпадає з кривою ао, а пройде значно вище- крива ав. Індукція В2=ов називається залишковою.
Розглянемо цю залежність. Якщо повністю розмагнечений феромагнітний зразок внести в магнетне поле то при рівномірному збільшенні напруженості магнетного поля залежність В від Н зображається дільницею оа (рис.1), яка носить назву основної кривої намагнечування. При подальшому збільшенні напруженості поля Н ця крива переходить в лінійну залежність, так як намагнеченість досягає насичення і залишається сталою, а В зростає тільки за рахунок збільшення Н, при зменшенні Н до нуля крива розмагнечування не співпадає з кривою ао, а пройде значно вище- крива ав. Індукція В2=ов називається залишковою.
Для знищення залишкової намагнеченості необхідно прикласти обернене поле напруженістю Нс=ос, яка називається коерцитивною силою.
При подальшому збільшенні оберненого поля знову досягається насичення. Якщо від точки насичення d зменшувати магнетне поле до нуля, а далі, змінивши напрямок Н, збільшувати поле, одержимо криву намагнечування defa. Замкнена крива abcdefaносить назву петлі гістерезису. Явище гістерезису обумовлене доменною структурою феромагнетиків. Для середовища магнетне поле кількісно оцінюється відносною магнетною проникністю
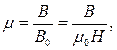 (1)
(1)
де В –індукція магнетного поля в речовині;
В0 – індукція зовнішнього поля (намагнічуючого).
У зв’язку з тим, що в феромагнетиках залежність В від Н неоднозначна, поняття відносної магнетної проникності m застосовується лише до основної кривої намагнечування і, як випливає з вигляду цієї кривої, в свою чергу залежить від Н.
Величини В2,Нс, mє основними характеристиками феромагнетиків. Якщо коерцитивна сила Нс велика, то феромагнетик називається жорстким, для нього характерна широка петля гістерезису. Феромагнетик з малою Нс (в нього відповідно вузька петля ) називають м'яким.

Рис. 2.
На рис.2. зображена схема для спостереження петлі гістерезису на екрані осцилографа, де осердям тороїда служить досліджуваний феромагнетик. Щоб одержати на екрані осцилографа петлю гістерезису, необхідно на горизонтальні відхиляючі пластини подати напругу Ux, яка пропорційна напруженості магнетного поля H досліджуваного зразка, а на вертикально відхиляючі пластини- напругу Uy, пропорційну векторові магнетної індукції В.
Доведемо виконання цих умов у даній схемі. Напруга Ux подається на осцилограф з опору R1, через який проходить струм I1, що живить первинну обмотку тороїда, який створює магнетне поле H для намагнечування зразка, а величина магнетного поля пропорційна струмові. Таким чином, напруга Ux пропорційна H .
Напруга Uy подається на осцилограф з конденсатора С,який заряджається завдяки ЕРС індукції, що виникає на вторинній обмотці тороїда. Величина ж ЕРС індукції залежить від магнетного потоку, який визначається через вектор індукції магнетного поля. Таким чином, напругаUy пропорційна магнетній індукції В.
Точні розрахунки дають такі співвідношення:
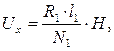 (2)
(2)
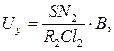 (3)
(3)
де N1 – повне число витків первинної (намагнечуючої) обмотки;
l1 – довжина первинної обмотки;
S –площа перерізу тороїда;
N2 – повне число витків вторинної (індикаторної) обмотки;
l2 – довжина вторинної обмотки;
С – ємність конденсатора.
Таким чином, на горизонтально відхиляючі пластини осцилографа подається напруга Ux,пропорційна H, а на вертикально відхиляючі – Uy пропорційна B. В результаті на екрані одержуємо петлю гістерезису B=¦(H).
За один період синусоїдальної зміни струму електронний промінь на екрані описує повну петлю гістерезису, а за кожний наступний період точно її повторює. Тому на екрані спостерігається нерухома петля. Збільшуючи потенціометром r напругу Ux, збільшуємо амплітуду Ні одержуємо на екрані різні за своєю площею петлі гістерезису. Верхня точка кожної такої петлі (точка aна рис.1.) знаходиться на початковій (основній) кривій намагнечування. Тому для одержання основної кривої намагнечування (кривої oa на рис.1.) необхідно зняти з екрану осцилографа координати nx i nyвершин петель гістерезису при різних напругах Ux.
Порядок виконання роботи
Завдання 1. Зняття основної кривої намагнечування.
1. Зібрати схему за рис. 2.
2. Ввімкнути осцилограф i вивести електронний промінь на центр координатної сітки.
3. Після перевірки схеми викладачем або лаборантом ввімкнути її в мережу.
4. За допомогою ручок “Підсилення по вертикалі”, “Підсилення по горизонталі” та потенціометром r добитися, щоб петля гістерезису мала ділянку насичення і займала значну частину екрану.
5. Визначити координати nxi ny вершини петлі (координата точки a на рис.1.)
6. Зменшити напругу за допомогою потенціометра r; одержати ряд петель i для кожної з них записати координати вершин. Вимірювання проводити до тих пір, поки петля не стягнеться в точку.
7. Повторити пп 5, 6 для інших феромагнетиків.
Завдання 2. Одержання петлі гістерезису
1. Виконати вимоги згідно пунктів 1 — 4 “Завдання 1”.
2. Одержати координати 15—20 різних точок петлі в поділках координатної сітки екрана осцилографа.
3. Намалювати петлю на міліметровому папері, вибравши на осях хі y такий же масштаб, як і на координатній сітці осцилографа.
Контрольні запитання
1. Дайте пояснення явищам, які відбуваються в речовині при внесені її в магнетне поле.
2. Подайте основи елементарної теорії діа— і парамагнетизму.
3. Назвіть основні особливості магнетних властивостей феромагнетиків.
4. В чому полягає суть явища гістерезису?
Лабораторна робота №3-9
Визначення точки Кюрі феромагнетика
л. 1. §59.2. §§20.6,20.7
Мета роботи: набути навиків вимірювання температурної залежності намагнеченості феромагнетика.
Прилади та матеріали: електрична піч; феромагнітний зразок;мікроампер-метр; мілівольтметр; термопара.
Теоретичні відомості
У загальному випадку вектор магнетної індукції в середовищі зв’язаний з напруженістю магнетного поля співвідношенням:
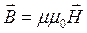 (1)
(1)
де 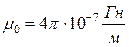 – магнетна стала;
– магнетна стала;
m – відносна магнетна проникність середовища (для вакууму m=1)
Магнетна індукція в середовищі визначається магнетною індукцією в вакуумі В0=m0Н і намагнеченістю середовища m0j

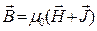 (2)
(2)
де 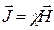 – вектор намагнечування, рівний магнетному моменту одиниці об’єму речовини;
– вектор намагнечування, рівний магнетному моменту одиниці об’єму речовини;
c – магнетна сприйнятливість середовища.
Перепишемо (2):
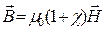 (3)
(3)
При порівнянні (1) і (2) виходить, що
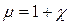 (4)
(4)
Якщо c<0; m<1, то речовини називаються діамагнетиками. Речовини, для яких c>0; m>1,називаються парамагнетиками. Діа- і парамагнетики належать до класу слабомагнітних речовин, їх магнетна проникність близька до одиниці.
Речовини, які здатні сильно намагнечуватись називаються феромагнетиками.
Основні властивості діа-, пара- і феромагнетиків розглянуті в теоретичних відомостях до лабораторної роботи № 3-7. В даній лабораторній роботі вивчається залежність основних характеристик магнетиків від температури.
На основі класичних уявлень одержані такі формули для mі cв діамагнетиках:
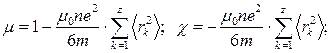 (5)
(5)
де е=1,6×10-19 Кл – заряд електрона;
m=9,1×10-31 кг – маса електрона;
z – число електронів в атомі;
n – число атомів в одиниці об’єму;
<rк2> – квадрат середньої відстані к-го електрона від ядра.
Квантово-механічна теорія феромагнетизму приводить до точно таких же висновків. Із (5) витікає, що m і c діамагнетиків не залежить від температури. Відмітимо також, що значення m і c розраховані за формулами (5), добре співпадають з експериментальними результатами.
Кюрі експериментально установив закон, згідно з яким залежність магнітної сприйнятливості парамагнетиків від температури визначається за формулою:
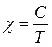 (6)
(6)
деС – стала Кюрі;
T – абсолютна температура.
Класична теорія парамагнетизму була розвинена в 1905 році. Згідно цієї теорії:
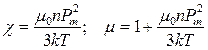 (7)
(7)
де k – стала Больцмана;
рm – магнетний момент атома.
Із (7) і(6) слідує, що стала Кюрі
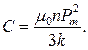 (8)
(8)
Слід відмітити, що формули (7) справедливі для не досить сильних полів (рmв<<кТ) і для дуже низьких температур. Значення m і c розраховані за формулами (7), в ряді випадків добре співпадають з експериментом. Квантова теорія парамагнетизму враховує, що можливі лише дискретні орієнтації рm, відносно поля, однак і вони приводять до виразів, аналогічних0 (7).
Експериментально установлено, що для кожного феромагнетика є відповідна температура Тс, при якій області спонтанного намагнечування (домени) руйнуються і речовина втрачає феромагнітні властивості. Ця температура називається точкою Кюрі. Для кожного феромагнетика вона має своє цілком визначене значення; наприклад, для заліза Тс=468°С, для нікелю-Тс=365°С, тощо. При температурі, вищій за точку Кюрі, феромагнетик стає звичайним парамагнетиком, магнетна сприйнятливість пояснюється законом Кюрі-Вейса:
Дата добавления: 2015-10-09; просмотров: 1389;
