Лабораторна робота № 2-6 3 страница
3. Ввімкнути котушку на N = 100 витків і, змінюючи струм реостатом R, добитися відхилення стрілки на 45°. Записати значення струму I1¢ .
4. Перемикачем П змінити напрямок струму в котушці і знову добитись відхилення стрілки на 45° в протилежний бік. Записати значення струму I2¢.
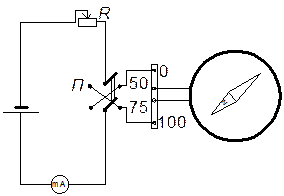
Рис.4
5. Перевірити нульове встановлення приладу і повторити виміри для N2=75 i N3=50 витків. Записати значення струмів I1", I1¢¢¢, I2¢¢, I2¢¢¢.
6. Штангенциркулем виміряти середній діаметр витків котушки.
Додаткове завдання.
1. Перевірити, експериментально, справедливість рівності 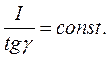
2. Дослідити вплив кута відхилення стрілки g на точність визначення Н0 .
Обробка результатів експерименту та їх аналіз
1. Обчислити значення постійних С як середнє значення струмів:
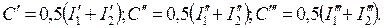
2. За формулою(5) обчислити Н0¢, Н0¢¢, Н0¢¢¢.
3. Розрахувати середнє значення Н0,абсолюту DН0 і відносну E похибки по результатах трьох вимірювань.
4. Обгрунтувати вибраний в даній роботі кут повороту стрілки на 45°, провівши аналіз формули відносної похибки, одержаної з робочої формули, записаної у вигляді:
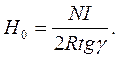
Контрольні запитання.
1. Елементи земного магнетизму.
2. Природа земного магнетизму.
3. Cформулювати закон Біо-Савара-Лапласа.
4. Вивести формулу для напруженості магнетного поля в центрі і на осі колового струму.
5. Пояснити будову і принцип дії тангенс-гальванометра.
6. . Чому виміри проводились при куті відхилення g= 45° ?
Лабораторна робота №3-3
Визначення питомого заряду електрона методом магнетного фокусування
л. 1. §§41,43. 2. §§18.1,18.2,18.3,18.4
Мета роботи: визначити питомий заряд електрона з допомогою магнетного фокусування розбіжного електронного пучка.
Прилади та матеріали: електронно-променева трубка з блоком живлення; джерело постійного і змінного струмів; реостат; амперметр; вольтметр.
Теоретичні відомості
Питомий заряд електрона є важливою характеристикою, знання якого необхідне при розрахунках конструкцій різних електровакуумних приладів, електронно-оптичних установок, прискорювачів і т.д. Експериментальні методи визначення e/mзасновані на законах руху електронів в електричних і магнетних полях. Ці ж методи використовуються і для визначення маси частинок, якщо відомий їх заряд або заряду при відомій масі.
У даній лабораторній роботі використовується метод фокусування пучка електронів поздовжнім магнетним полем. Принципова схема установки показана на рис. 1.
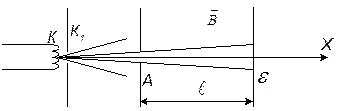
Рис.1
Електрони, які вилетіли з нагрітого катоду К, прискорюються електричним полем, створеним між катодом і анодом А , входять через малий отвір в аноді розбіжним променем і, попавши на флуоресціюючий екран e створюють світлу пляму.
 Якщо в просторі між анодом і екраном Ee створити магнетне поле з індукцією B , направленою вздовж осі x, то на електрон, який рухається в цьому полі з швидкістю
Якщо в просторі між анодом і екраном Ee створити магнетне поле з індукцією B , направленою вздовж осі x, то на електрон, який рухається в цьому полі з швидкістю 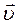 , буде діяти сила Лоренца:
, буде діяти сила Лоренца:
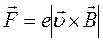 (1)
(1)
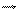 Сила F перпендикулярна як до напряму магнетного поля, так і до напряму руху електрона. Для електрона е < 0, тому сила буде направлена так, як показано на рис. 2.
Сила F перпендикулярна як до напряму магнетного поля, так і до напряму руху електрона. Для електрона е < 0, тому сила буде направлена так, як показано на рис. 2.
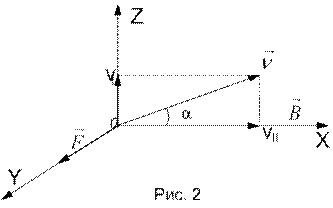
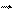 Якщо напрям руху електрона і магнетна індукція створюють кут a, то швидкість
Якщо напрям руху електрона і магнетна індукція створюють кут a, то швидкість 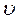 можа розкласти на дві складові, одна із яких перпендикулярна, а інша паралельна магнетному полю:
можа розкласти на дві складові, одна із яких перпендикулярна, а інша паралельна магнетному полю:
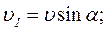
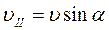 (2)
(2)
Запишемо формулу (1) в скалярній формі
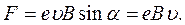 (3)
(3)
Таким чином, значення сили Лоренца визначається тільки нормальною складовою швидкості.
Розглянемо рух електронів як складний рух з швидкостями 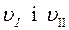 . Для випадку однорідного поля (B=const) числові значення
. Для випадку однорідного поля (B=const) числові значення 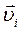 і сили, діючої на електрон в цьому напрямку, залишаються незмінними .
і сили, діючої на електрон в цьому напрямку, залишаються незмінними .
Тому проекція траєкторії електронів на площину zoyбуде колом. Паралельна складова швидкості електронів 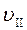 залишається постійною за абсолютною величиною і напрямом, так як магнетне поле не діє на частинку, яка рухається вздовж силових ліній.
залишається постійною за абсолютною величиною і напрямом, так як магнетне поле не діє на частинку, яка рухається вздовж силових ліній.
У даному випадку рух електронів здійснюється по гвинтовій лінії, тобто з постійною швидкістю вздовж осі хі по колу в площини zoy.
Визначимо крок гвинтової лінії l. За другим законом Ньютона:
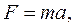
а врахувавши (3) і те, що 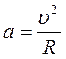 , одержимо
, одержимо 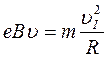 .
.
В результаті знаходимо радіус кола:
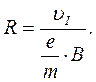 (4)
(4)
Очевидно, що час одного оберту:
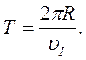 (5)
(5)
З формул (4) і (5) одержуємо:
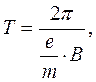 (6)
(6)
За час одного оберту електрон, рухаючись рівномірно вздовж осі х , пройде шлях, рівний кроку гвинтової лінії (рис. 3).
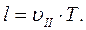 (7)
(7)
З формул (2), (6) і (7) одержуємо:
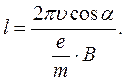 (8)
(8)
Так як в будь-якому випадку кут a надзвичайно малий, то cosa»1, а вираз (8) перепишеться:
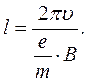 (9)
(9)
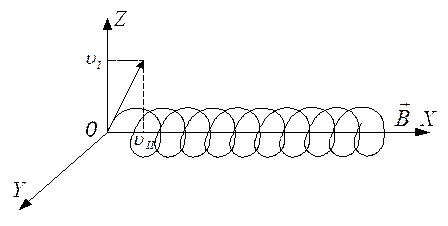
Рис.3
Це означає, що всі електрони, які вилетіли з отвору анода А з однаковою швидкістю за час Тв площині zoyописують повні кола і пере-міщуються вздовж осі х на віддаль l, тобто зберуться в одній точці (рис 4).
Потім електронний промінь знову розходиться і фокусується через новий проміжок часуТ в точці О2, яка віддалена від точки О на 2l т.д. У цьому полягає принцип фокусування електронних променів. Співвідношення (9) може бути використане для визначення питомого заряду електрона:
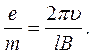 (10)
(10)
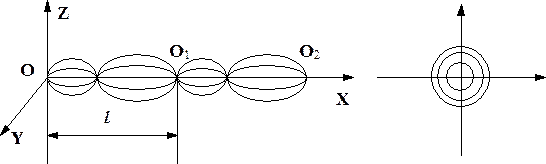
Рис.4.
Початкова швидкість електронів, що емітуються катодом нехтується, завдяки великим значенням анодної напруги U. Кінцева швидкість електронів визначається із співвідношення:
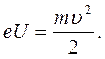 (11)
(11)
Із виразів (10) і (11) одержуємо остаточну формулу для експериментального визначення питомого заряду електрона 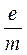 :
:
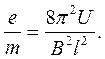 (12)
(12)
Як видно із (4) і (9) крок гвинтової лінії і її радіус залежать від індукції B магнетного поля, тому, якщо поле неоднорідне, гвинтова лінія буде мати змінний крок і радіус. Але і в цьому випадку, якщо поле циліндрично симетричне, тобто джерело електронів розміщене на осі симетрії ох, кут aдля всіх електронів буде практично однаковим. Проекції траекторій електронів на площину zoyбудуть у цьому випадку еліптичними, а не коловими, як показано на рис.4.
Теорія методу
Для вимірювання величини e/mвикористовується установка, схема якої показана на рис.5. Основна частина установки— електронно- променева трубка.
Електрони, що вилітають з нагрітого катода K, проходять через фокусуючий електрод К1 , а потім отвір в аноді і рухаються далі з постійною по величині швидкістю, значення якої визначається прискорюючою напругою U. Потім пучок електронів попадає в змінне електричне поле відхиляючих пластин С, направлене перпендикулярно до осі променя. Після конденсатора електрони попадають на екран трубки, покритий флуоресціюючою речовиною (ZnS) Точки екрану, на які попадають електрони, світяться, так-як при цьому атоми флуоресціюючої речовини збуджуються і на екрані створюється світла смуга.
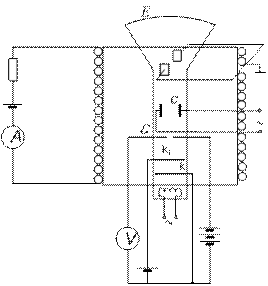
Щоб кут a був достатньо малим, довжина світлої смужки на екрані не повинна перевищувати 1,5-2 см. Електронно-променева трубка встановлена в середину соленоїда, що створює поздовжнє магнетне поле напруженістю Н , паралельне осі ох:
H = n I,
де I – струм в соленоїді;
n – число витків на одиницю довжини соленоїда. Під дією цього магнітного поля і відбувається фокусування електронного пучка, тобто електрони, збираються в одній точці (точка 01, на рис. 4). Відповідною зміною струму I в соленоїді, а значить і індукції магнетного поля
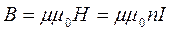 (13)
(13)
можна добитись того, щоб точка О1 співпала з екраном.
Тоді l буде дорівнювати віддалі між відхиляючими пластинами C і екраном E і залишається ста-лою величиною для даної точки.
Таким чином, вираз (12) з урахуванням (13) набуває вигляду:
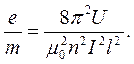 (14)
(14)
Порядок виконання роботи
1. Зібрати схему згідно рис.5. Після перевірки схеми лаборантом або викладачем ввімкнути її в мережу 220 В.
2. Ввімкнути джерело живлення електронно-променевої трубки. На екрані з’явиться світла смужка. Вертикально-відхиляючі пластини в цьому випадку повинні бути заземлені.
3. Замкнути ключ і підібрати з допомогою реостата такий струм в соленоїді, щоб світла смужка на екрані була зведена в точку.
4. Зняти покази амперметра і вольтметра.
Обробка результатів експерименту і їх аналіз
1. Розрахувати питомий заряд електрона за формулою (14). Значення n i lвказані на панелі установки.
2. Порівняти одержаний результат e /m з табличним значенням і пояснити причини розходження цих результатів.
Контрольні запитання
1. Подайте суть використаного в даній роботі методу магнітного фокусування електронних пучків.
2. Як знаходять радіус і крок гвинтової лінії, вздовж якої рухаються електрони?
Лабораторна робота № 3-4
Визначення напруженості магнетного поля на
осі соленоїда
л. 1. §50.2. §§15.4, 15.5
Мета роботи: набути навиків вимірювання напруженості магнетного поля в різних точках вздовж осі соленоїда.
Прилади та матеріали: соленоїд з вимірювальною котушкою; балістичний гальванометр; амперметр; реостат; вимикач.
Теоретичні відомості
Напруженість магнетного поля на осі соленоїда в загальному випадку визначається за формулою:
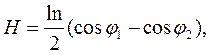 (1)
(1)
де I – струм, що проходить по обмотці соленоїда;
n – кількість витків на одиницю довжини соленоїда;
j1 та j2– кути під якими з точки спостереження видно радіуси поблизу кінців соленоїда (рис.1).
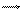
 Коли діаметр і довжина соленоїда сумірні то такий соленоїд називається коротким. Для короткого соленоїда напруженість Нмагнетного поля максимальна на осі соленоїда. В решті точок величина Н менша.
Коли діаметр і довжина соленоїда сумірні то такий соленоїд називається коротким. Для короткого соленоїда напруженість Нмагнетного поля максимальна на осі соленоїда. В решті точок величина Н менша.
Для довгого соленоїда ( коли R<<l) j1® 0 , j2 ®pі магнітне поле буде однорідним. Обчислимо напруженість магнетного поля для будь-якої точки на осі соленоїда.
З рис.1 видно, що
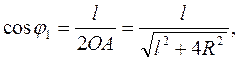 (2)
(2)
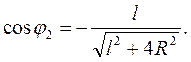 (3)
(3)
Тоді 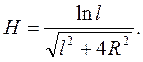 (4)
(4)
Величина n ×l = N – повне число витків. Отже,
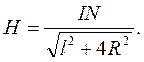 (5)
(5)
Поле багатошарового соленоїда якісно має той самий характер, як і поле одношарового.
У даній роботі напруженість магнетного поля визначається за допомогою балістичного гальванометра. Схему установки наведено на рис. 2. Балістичний гальванометр приєднується до вимірювальної котушки W. При замиканні вимикача К напруженість магнетного поля на осі соленоїда зростає від нуля до значення Н.
Магнетний потік, який пронизує при цьому вимірювальну котушку:
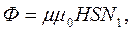 (6)
(6)
де S і N1– площа поперечного перерізу і число витків вимірювальної котушки.
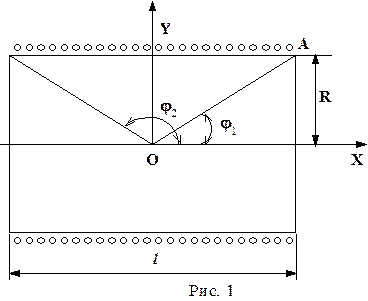
У колі котушки W виникає короткочасний індукційний струм і рамка гальванометра відхиляється на деякий кут b. Зміщення світлового “зайчика” відраховується по шкалі гальванометра.
Кількість електрики q, що пройде через гальванометр,
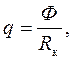 (7)
(7)
де Rk- опір кола гальванометра, Ом. (Складається з опору котушки і опору гальванометра) 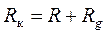 .
.
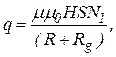 (8)
(8)

З другого боку, кількість електрики q пропорційна величині зміщення покажчика балістичного гальванометра від положення рівноваги a:
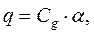 (9)
(9)
де Сg– стала балістичного гальванометра (рівна ціні однієї поділки шкали балістичного гальванометра).
З формул (8) і (9) маємо:
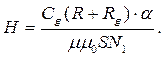 (10)
(10)
Величини S, N1, R, Rg, Cg, залишаються сталими при всіх вимірюваннях, тому введено позначення:
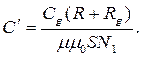 (11)
(11)
тоді
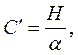 (12)
(12)
де С¢ – балістична стала установки.
Після визначення сталої С¢ установки можна визначити напруженість магнетного поля в будь-якій точці, розміщеній на осі соленоїда
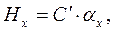 (13)
(13)
де індекс хозначає координату на осі соленоїда.
Порядок виконання роботи
1. Скласти схему згідно рис. 2.
2. Розмістити вимірювальну котушку W на осі соленоїда, що відповідає координаті х = 0, та встановити реостатом струм у колі соленоїда 1,0-1,5 А. (За точку відліку прийняти точку, яка розміщена в центрі соленоїда)
3. Розрахувати напруженість магнітного поля на осі соленоїда (центр соленоїда) за формулою (5).
4. Визначити a в момент замикання та розмикання і взяти середнє значення.
5. Користуючись формулою (11), визначити сталу С¢
6. Повторити вимірювання, зазначені в пп. 4,5, не менше як 3 рази та розрахувати середнє значення.
7. Провести вимірювання в точках соленоїда, розташованих одна від одної на відстані 1 см. від точки х=0 і до точки, яка співпадає з кінцем соленоїда.
8. Записати в таблицю .для кожної точки значенння aх та за формулою (13) розрахувати напруженість магнітного поля в цих точках.
9. Побудувати графік залежності Нх від х. Початок координат сумістити з точкою в центрі соленоїда.
Контрольні запитання
Сформулюйте закон Біо-Савара-Лапласа.
Виведіть формулу для Н на осі колового витка і на осі соленоїда.
Лабораторна робота №3 - 5
Визначення індуктивності соленоїда
л. 1. §50. 2. §§15.4,15.5
Мета роботи: засвоєння навичок експериментального визначення індуктивності соленоїда та дослідження залежності індуктивності від магнітних властивостей осердя і сили струму.
Прилади та матеріали: дві котушки із спільним рухомим осердям; амперметр; вольтметр; ватметр; автотрансформатор; омметр.
Теоретичні відомості
Явище виникнення електричного струму в замкнутому контурі при зміні магнетного потоку, що охоплений контуром провідника, називається електромагнітною індукцією. Струм, який виникає в провідникові, називається індукційним.
Але струм провідності в замкненому колі може виникнути лише під дією стороннього електричного поля. Звідки випливає, що в замкненому контурі під дією змінного магнетного поля виникає електричне поле. Енергетичною характеристикою цього поля є електрорушійна сила (ЕРС) електромагнетної індукції εі , величина якої визначається законом Фарадея:
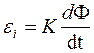 (1)
(1)
де К – коефіцієнт пропорційності, величина якого залежить від вибору системи одиниць;
Ф = B ×S ×cosa– магнетний потік через поверхню S охоплену контуром;
 a – кут між зовнішньою нормаллю до поверхні S і вектором індукції магнетного поля B.
a – кут між зовнішньою нормаллю до поверхні S і вектором індукції магнетного поля B.
Закон Фарадея доповнюється законом Лєнца, згідно з яким при всякій зміні магнетного потоку через поверхню, яка охоплена замкненим контуром, в останньому виникає індукційний струм такого напрямку, що його магнетне поле протидіє зміні магнітного потоку. Враховуючи це і беручи всі величини в формулі (1) в одиницяхСІ (при цьому К=-1), закон електромагнетної індукції запишемо в кінцевому вигляді:
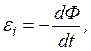 (2)
(2)
тобто, електрорушійна сила електромагнетної індукції дорівнює швидкості зміни магнетного потоку з протилежним знаком.
Явище електромагнетної індукції має місце у всіх випадках зміни магнетного потоку, охопленого контуром. Зокрема, цей потік може створюватись струмом, що протікає в самому контурі. Тому при зміні сили струму в якому-небудь контурі в ньому ж виникає ЕРС індукції, яка викликає додатковий струм в контурі. Це явище носить назву самоіндукції, а електрорушійна сила- ЕРС самоіндукції. Розглянемо, від чого вона залежить. Величина магнетного поля в будь-якій точці пропорційна силі струму І в контурі, тому й магнітний потік Ф , охоплений контуром, пропорційний струмові:
Ф = LI . (3)
Коефіцієнт пропорційності L називається індуктивністю контура. За одиницю індуктивності приймається 1 генрі (Гн). Це індуктивність такого контура, в якому при силі струму 1 А виникає магнітний потік 1 Вб:
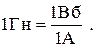
Застосовуючи до явища самоіндукції основний закон електромагнітної індукції (2), одержимо для ЕРС самоіндукції вираз:
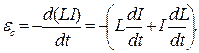 (4) Визначимо індуктивність безмежно довгого соленоїда. Напруженість магнетного, поля всередині такого соленоїда:
(4) Визначимо індуктивність безмежно довгого соленоїда. Напруженість магнетного, поля всередині такого соленоїда:
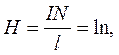 (5)
(5)
де N – загальне число витків;
l – довжина соленоїда;
n – число витків на одиницю довжини соленоїда.
Якщо площа перерізу соленоїда S, то магнетний потік через один виток буде:
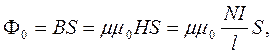
а повний потікчерез всі N витків:
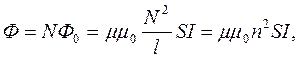 (6)
(6)
Співставляючи формули (6) і (3), приходимо до висновку, що індуктивність соленоїда:
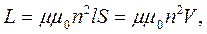 (7)
(7)
де V – об’єм соленоїда.
Таким чином, ми переконались, що індуктивність залежить від форми та розмірів контура, а також від магнітних властивостей m навколишнього середовища. Якщо навколишнє середовище є феромагнетиком, то m складна функція від І, тому і залежність L від I досить складна. Якщо ж m не залежить від I, тобто при відсутності феромагнетика, тоді L=const і формула (4) набуває вигляду:
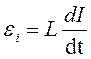 (8)
(8)
Розглянемо електричне коло, яке складається з послідовно з’єднаних резистора R, індуктивності L та ємності С (Рис. 1). Ввімкнемо в це коло змінну напругу, яка описується законом:
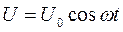 (9)
(9)
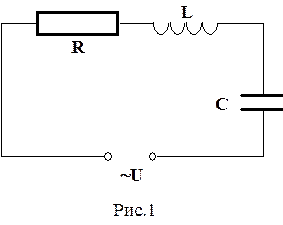
У колі виникне струм тієї ж частоти амплітуда I0 і фаза j якого, очевидно, визначатиметься параметрами R, L та С. Напруги на окремих ділянках кола описуватимуться рівняннями:
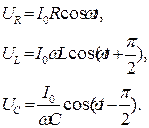 (10)
(10)
Напруги UR, UL, UCв сумі повинні дорівнювати прикладеній в колі напрузі U. Визначимо цю суму за допомогою векторної діаграми (Рис. 2).
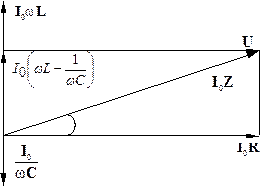
Рис.2.
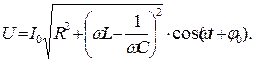 (11)
(11)
Величина
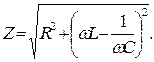 (12)
(12)
називається повним опором кола, а величина
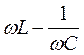 (13)
(13)
реактивним опором.
Зсув фаз j між струмом і напругою можна визначити із співвідношення:
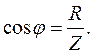 (14)
(14)
З формули (11) випливає, що амплітудне значення напруги дорівнює:
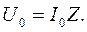 (15)
(15)
Слід відмітити, що активний опір R визначає витрати електричної енергії на нагрівання. Якщо нема осердя, то активний опір дорівнює омічному опорові провідників R0. При наявності феромагнітних осердь виникають додаткові витрати, обумовлені вихровими струмами та гістерезисними явищами. Таким чином, у загальному випадку активний опір більший омічного, тобто більший за опір постійному струмові.
Відомо, що потужність у колах змінного струму може бути знайдена через амплітудні, а також через ефективні значення струму та напруги:
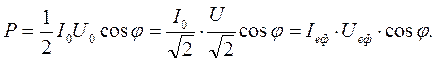 (16)
(16)
При цьому зауважимо, що закон Ома в формулі (15) справедливий також і для ефективних значень струму та напруги:
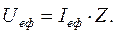 (17)
(17)
Підставивши вирази (14) та (17) в (16) одержуємо:
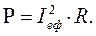 (18)
(18)
Тобто, в досліджуваному нами колі змінного струму середня в часі потужність обумовлена наявністю активного опору. Проходження струму через ємність і індуктивність супроводжується взаємним перетворенням енергії електричного поля конденсатора та магнетного поля соленоїда з періодичним поверненням її в джерело струму. У цій лабораторній роботі вивчається коло, що складається з індуктивності та активного опору, а ємність кола настільки мала, що в розрахунках не враховується.
Порядок виконання роботи
1. Зібрати схему (Рис. 3). Одержати вказівки у викладача чи лаборанта, при яких струмах слід проводити експеримент.
2. Заміряти омметром омічний опір соленоїда R0.
3. Заміряти величину струму Iеф, що проходить через соленоїд при трьох різних значеннях напруги Uеф на його кінцях.
4. Вставити в соленоїд осердя і записати покази ватметра Р, амперметра I¢еф та вольтметра U¢еф
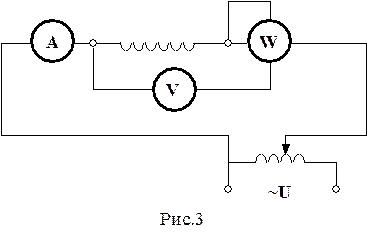
.
Обробка результатів експерименту та їх аналіз.
1. З трьох значень Uефі Iеф за формулою(17) вирахувати повний опір кола Z та знайти його середнє значення Zcp.
1. За формулою 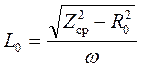 визначити індуктивність соленоїда без осердя. Ця формула одержана з виразу (12) при умові, що ємність у колі відсутня; w = 2pn, n= 50 Гц - частота струму в міській мережі.
визначити індуктивність соленоїда без осердя. Ця формула одержана з виразу (12) при умові, що ємність у колі відсутня; w = 2pn, n= 50 Гц - частота струму в міській мережі.
2. Знайти повний опір соленоїда з осердям за формулою :
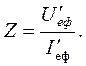
3. Визначити активний опір соленоїда, користуючись формулою:
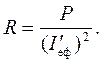
4. Знайти індуктивність соленоїда з осердям:
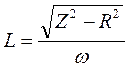
5. Пояснити різницю між L та L0 .
Контрольні запитання
1. Пояснити суть явища електромагнітної індукції.
2. Пояснити суть явища самоіндукції.
3. Як знаходять індуктивність котушки та від яких параметрів вона залежить?
4. Що таке активний опір контура, реактивний опір?
5. Користуючись векторною діаграмою, знайдіть напругу в колі змінного струму, яке містить окремо омічне, індуктивне а6о ємнісне навантаження.
Лабораторна робота №3-6
Вивчення явища взаємної індукції
л. 1. §66. 2. §19.5
Мета роботи: дослідження явища взаємної індукції двох коаксіально розміщених котушок.
Прилади та матеріали: звуковий генератор, осцилограф, дві коаксіальні котушки індуктивності, стержень зі шкалою.
Теоретичні відомості
Розглянемо два контури 1 і 2, які розміщені на деякій віддалі один від одного ( Рис.1). Якщо по контуру 1 пропустити струм I1, то він створює потік магнетної індукції через контур 2, який буде пропорційний струму I1:

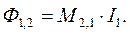 (1)
(1)
Коефіцієнт пропорційності M2,1 називається коефіцієнтом взаємної індукції контурів. Він залежить від форми і взаємного розміщення контурів 1 і 2, а також від магнетних властивостей навколишнього середовища. При зміні струму в першому контурі магнетний
потік через другий контур змінюється, а це значить, що в ньому наводиться ЕРС взаємної індукції:
Дата добавления: 2015-10-09; просмотров: 1574;
