Лабораторна робота № 1-9 5 страница

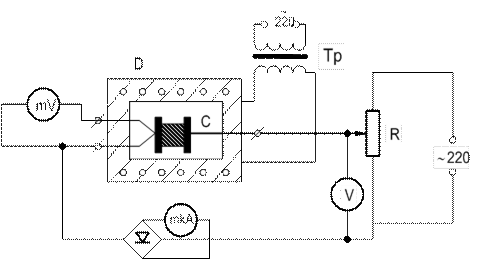
Рис. 11

На рис. 11 зображена електрична схема експериментальної установки для дослідження температурної залежності відносної діелектричної проникності титанату барію, який є сегнетоелектриком в області температур від 5 до 120°С.

Конденсатор С складається з круглої пластинки титанату барію товщиною d=1 мм і діаметром D=8 мм, яка розміщена в фарфоровій трубці. Пластинка в трубці стиснена двома металевими електродами циліндричної форми, що служать обкладками плоского конденсатора. До одного з електродів приєднана хромонікелева термопара, один з провідників якої є одночасно струмонесучим провідником в колі мікроамперметра. Термо-ЕРС вимірюється мілівольтметром, а відповідна їй температура визначається з градуювального графіка для даного типу термопар, який додається до роботи. Потенціометром R встановлюється необхідна напруга U для живлення схеми. Детекторами в схемі мікроамперметра служать напівпровідникові діоди Д226Г. Живлення пічки Д здійснюється від знижуючого трансформатора Тр 220/150 В.

Мікроамперметр фіксує середнє значення випрямленого струму I_C , але для розрахунку кіл змінного струму необхідно знати ефективне значення струму в колі I_еф , в цьому випадку слід враховувати перехідний коефіцієнт:

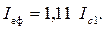(1)

Розглянемо методику знаходження відносної діелектричної про­никності сегнетоелектрика та дослідження її температурної залежності з допомогою даної установки. Нехай при кімнатній температурі t₁⁰ефективне значення струму в колі при напрузі U буде I₁. При цьому мікроамперметр дасть значення I_C1. На основі закону Ома запишемо:

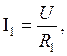(2)

де 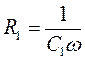— ємнісний опір кола змінного струму з циклічною частотою;

w=2p¦, ¦=50 Гц — частота струму міської мережі.

Електричну ємність C₁ знайдемо як ємність плоского конденсатора:

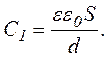(3)

Враховуючи вирази для R₁ і C₁ із формули (2) знайдемо відносну діелектричну проникність сегнетоелектрика e₁ при кімнат­ній температурі:

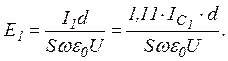(4)

де e₀ = 8,85 10^-12 Ф/м - електрична стала.

При підвищенні температури зразка його відносна діелектрична проникність зміниться і набуде значенняe , причому, як випливає з формули (4):

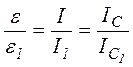(5)

тобто, надалі розрахунки та дослідження можна проводити, викорис­товуючи тільки покази мікроамперметра середніх значень струму, не переводячи в ефективне.

Порядок виконання роботи

1. При кімнатній температурі t₁^° ввімкнути коло конденсатора в мережу через потенціометр R. Встановити робочу напругу 100-120 В.

2. Записати значення напруги U і струму I_U .

3. Ввімкнути електропічку D через трансформатор Тр в мережу.

4. Через кожні п’ять поділок шкали мілівольтметра (через 0,5 мВ при його ввімкненні на 15 мВ) записувати значення струму мікроамперметра до тих пір, поки його покази повільно зростають.

5. Коли значення струму почнуть спадати, покази мікроамперметра фіксувати через кожну поділку шкали мілівольтметра.

6. При досягненні температури 140°C, що відповідає 8,75 мВ, дослід припинити, пічку вимкнути і відкрити її верхню половину для остигання.

7. Користуючись градуйованим графіком термопари, перевести всі значення термо-ЕРС в градуси шкали Цельсія і скласти таблицю тем­ператур з відповідними їм значеннями струму.

Обробка результатів експерименту

1. За формулою (4) вирахувати відносну діелектричну проникність сегнетоелектрика e₁ при кімнатній температурі.

2. Користуючись співвідношенням (5), визначити відношення 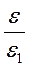для всіх значень струму.

3. Побудувати температурну залежність 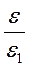і визначити точку Кюрі для даного сегнетоелектрика.

4. Знайти абсолютну та відносну похибки визначення відносної про­никності сегнетоелектрика, проаналізувати результати роботи та зробити висновки.

Контрольні запитання

1. Які основні властивості і будова сегнетоелектриків?

2. Залежність діелектричної проникності сегнетоелектриків від температу-ри. Що таке точка Кюрі?

3. Наведіть приклади застосування сегнетоелектриків в техніці і, зокрема, в Вашій майбутній спеціальності.

4.

Лабораторна робота № 2-5

Визначення електрорушійної сили джерела струму

л. 1. §33. 2. § 9.1

Мета роботи: набути навиків вимірювання електрорушійної сили джерел струму компенсаційним методом.

Прилади та матеріали: джерело струму; реохорд; нормальний елемент; гальванометр; досліджуване джерело струму.

Теоретичні відомості

При наявності замкнутого кола електричний струм існує лише до тих пір, поки між двома точками кола підтримується різниця потенціалів. Тому в замкнутому колі поряд з дільницями, на яких додатні заряди рухаються в сторону зменшення потенціалу j, повинні бути дільниці, на яких додатні заряди рухаються в зворотньому напрямі, тобто відбувається зростання потенціалу.

Таким чином, для підтримання струму в колі необхідні сторонні сили, які діють по всьому колу, або на його окремих ділянках і які створюють додаткові електричні поля. Напруженість стороннього поля Е_СТ вимірюється величиною сторонніх сил, які діють на одиничний додатний заряд

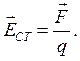
Вектор напруженості стороннього поля Ест всередині джерела на­прямлений проти вектора напруженості електростатичного поляЕ(рис.І). При розімкнутому зовнішньому колі електричне поле всередині джерелазрівноважується стороннім полем. Таким чином, джерело струму - це такий енергетичний агрегат, який концентрує від’ємні заряди на одній клемі, а додатні заряди на іншій. Ці заряди і створюють напругу на клемах розімкнутого джерела; вона чисельно дорівнює спаду напруги на внутрішньому опорі.

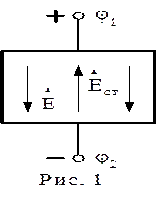
Сторонні сили виконують роботу по розділенню електричних за­рядів. Відношення величини роботи, яку виконують сторонні сили при переміщенні одиничного додатного заряду вздовж замкненого кола, до величини цього заряду, називають е.р.с. і вимірюють у вольтах (В) 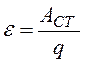(2)

Серед джерел струмів в лабораторній практиці велике поширення одержали гальванічні елементи, які виготовлені із таких речовин, що забезпечують значну постійність напруги на його клемах. Ця на­пруга була виміряна з великою точністю і тепер добре відома, тому так звані “нормальні гальванічні елементи” є зручними еталонами напруги, які легко відтворюються в будь-якій лабораторії. Кадмієвий нормальний гальванічний елемент при 20°С

має напругу на клемах 1,0186 В. При кімнатній температурі напруга цього елемента майже не залежить від температури: при підвищенні температури на І°С вона зменшується менше, як на 0,0001 В.

Будова кадмієвого нормального елемента подана на рис.2.

Від такого нормального елемента можна одержати надзви-чайно малі струми, однак вони цілком достатні для проведення різноманітних вимірювань.

Виявимо зв’язок між е.р.с. джерела і силою стрму в колі. Вважаючи, що джерелом струму є гальванічний елемент, узагальнимо одержані результати на випадок будь-якого джерела.

Якщо гальванічний елемент створює в колі струм, то всередині цього джерела відбувається хімічна реакція. Енергія хімічної реакції Q_Х і є та енергія, яка звільняється в гальванічних елементах. У випадку замкнутого кола в ньому буде виконуватись робота струму А , яка перетворюється в тепло:

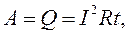(3)

При цьому слід враховувати, що електричні заряди ніде не нагро­маджуються в колі, а значить, струм існує не лише в зовнішньому колі, але і усередині джерела. Гальванічний елемент являє собою для струму деякий опір r, що називається внутрішнім, який скла­дається із опору електроліта і електродів.

Використавши, до розглянутого замкнутого кола, перший принцип термодинаміки (загальний закон збреження енергії), одержуємо:

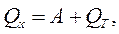(4)

де Q_T — деяка кількість теплоти, яка необхідна для підтримання постійної температури джерела.

Тоді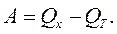

Величина А, являє собою частину енергіїQ_x, яку називають максимальною роботою хімічної реакції і яка пропорційна величині заряду, перенесеного по колу. Тому вважаючи e (2) максимальною роботою хімічної реакції (реакцій), розрахованої на одиницю заряду, і, прирівнявши її до величини роботи струму (в зовнішньому колі і в середині джерела), одержимо:

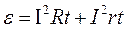
Розділивши обидві частини рівності на величину заряду одержимо:

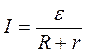(5)

Цей вираз носить назву закону Ома для замкнутого кола.

Величина максимальної роботи А , як і енергії хімічної реакції Q_Х, при відомій величині перенесеного заряду залежить тільки від розмірів джерела. Внутрішній же опір джерела, як і усього провідника, залежить від його розмірів і форми.

Е.р.с. гальванічного елемента можна подати і безпосередньо через тепловий ефект хімічної реакції. Ознайомитись з цим матеріалом можна з підручника фізичної хімії.

Одержаний закон Ома (5) при розгляданні джерела струму в вигляді гальванічного елемента має загальне значення, тому що всяке джерело можна охарактеризувати його електрорушійною силою. Напруга на затискачах джерела струму відповідно формулі (5) дещо менша е.р.с. джерела:

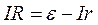(6)

Однак при значних за величиною опорах зовнішнього кола R порів­няно з внутрішнім опором джерела r спад напруги всередині джерела незначний і напруга на клемах наближається до е.р.с., тобто, якщо R>>r (коло розімкнуте), то e » U: електрорушійна сила рівна напрузі на клемах розімкнутого джерела. Такий метод вимірювання е.р.с. вважається досить наближеним.

Широке застосування одержав компенсаційний метод вимірювання е.р.с.. Цей метод досить простий, дає добру точність і реалізується в різноманітних типах потенціометрів. Принципіальна схема методу подана на рис. 3.

Основна ідея методу полягає в тому, що вимірювана е.р.с. зрівнова-жується (компенсується) спадом напруги на ділянці кола ВС так, що в результаті гальванометр показує відсутність струму в колі з невідомою е.р.с..

Запишемо рівняння Кірхгофа для схеми на рис.3, скориставшись позначеннями, вказаними в схемі:

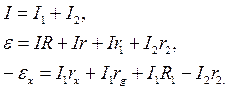(7)

Змінюючи опір r₂, можна досягти того, що струм I₁, в вибраній ділянці кола буде дорівнювати нулю. При цьому

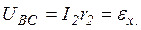(8)

Із співвідношення (8) видно, що регулювання компенсаційного спаду напруги 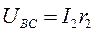можливе в двох випадках: при зміні струму I₂ або зміні опору r₂ . Перевагу в компенсаційних установках одержав другий випадок. При цьому в процесі вимірювань, струм, названий робочим струмом, підримується постійним. Із формули (8) також слідує, що точність методу залежить від точності установки робочого струму. Для даного методу велике значення має плавність регулювання опору r₂, якість і стабільність всіх опорів.

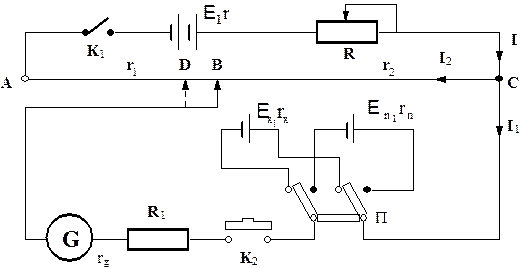
Рис .3.

Якщо в цю схему замість досліджуваного джерела струму e_х включити джерело e_n з відомою е.р.с., то з допомогою тих же міркувань можна одержати: 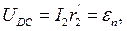(9)

де r₂^¢ – опір ділянки кола (реохорда DС).

Розділивши (8) на рівняння (9), одержимо формулу за якою можна визначити е.р.с.:

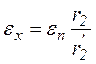(10)

Величина е.р.с. нормального елемента e_n відома із точністю до 10^-5 В. Опори ділянок реохорда r₂ і r₂^¢ можна замінити на довжини ділянок калібровочного дроту відповідно l₁=r_BCіl₂=r_DC. Тому робоча формула набуде вигляду:

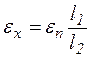(11)

Слід мати на увазі, що гальванометр реєструє відсутність струму, а не вимірює його, тому реєстрація факту компенсації не залежить від класу приладу, а залежить тільки від його чутливості.

Хід роботи

1. Скласти схему згідно рис.3, при цьому слід не переплутати напрямки увімкнення всіх е.р.с..

2. Перемикачем П ввімкнути в схему невідоме джерело E_х.

3. Добитись компенсації напруги U_всі е.р.с. невідомого елемента. Записати результати вимірювань.

4. Перемикачем П включити в схему нормальний елемент e_n.

5. З допомогою повзунка реохорда добитись відсутності струму через гальванометр.

6. Записати результати вимірювань.

7. З допомогою формули (11) розрахувати величину невідомої е.р.с..

Контрольні запитання

1. Дайте визначення е.р.с. джерела струму.

2. Як можна виміряти е.р.с. джерела струму.

3. Подайте суть компенсаційного методу вимірювання е.р.с..

4. Від чого залежить точність вимірювання е.р.с. компенсаційним методом.