Лабораторна робота № 1-9 3 страница
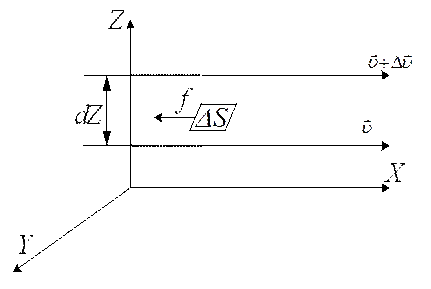
Розглянемо ріди-ну, що рухається в напрямку осі X (рис.1). Нехай шари рідини мають різну шви-дкість. Виберемо на осі Zдві точки, які розташовані одна від одної на віддалі dZ. Потік рідини цих точок за величиною швидкості відрізня-ється на dυ.
Співвідношення 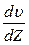 характеризує зміну швидкості потоку в напрямку осі Z і носить назву градієнта швидкості.
характеризує зміну швидкості потоку в напрямку осі Z і носить назву градієнта швидкості.
Сила внутрішнього тертя (в’язкості), що діє між двома шарами за законом Ньютона, пропорційна величині площі їх дотикання та
градієнта швидкості:
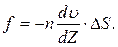 (1)
(1)
Величина h називається коефіцієнтом внутрішнього тертя або коефіцієнтом динамічної в’язкості. Якщо в формулі (1) взяти 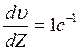 і
і 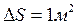 , тоді h=½f½, тобто коефіцієнт динамічної в’язкості чисельно дорівнює силі внутрішнього тертя, яка діє на одиницю площі двох шарів рідини, що дотикаються і рухаються один відносно другого з градієнтом швидкості, рівним одиниці. В системі СІ h вимірюється в одиницях кг×м-1×с-1.
, тоді h=½f½, тобто коефіцієнт динамічної в’язкості чисельно дорівнює силі внутрішнього тертя, яка діє на одиницю площі двох шарів рідини, що дотикаються і рухаються один відносно другого з градієнтом швидкості, рівним одиниці. В системі СІ h вимірюється в одиницях кг×м-1×с-1.
В системі СГС коефіцієнт динамічної в’язкості має розмірність г×см-1×с-1 і називається пуаз. Часто використовують одиницю в сто разів меншу —сантипуаз.
Коефіцієнт динамічної в’язкості залежить від природи рідини і з підвищенням температури зменшується. В’язкість грає суттєву роль в рухові рідини. Шар рідини, який безпосередньо прилягає до твердої поверхні, в результаті прилипання залишається відносно неї нерухомим. Швидкість решти шарів зростає з віддаленням від твердої поверхні. Наявність шарів рідини між поверхнями твердих тіл сприяє значному зменшенню коефіцієнта тертя.
Поряд з коефіцієнтом динамічної в’язкості h часто користуються поняттям коефіцієнту кінематичної в’язкості:
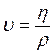 (2)
(2)
де r – густина рідини.
В системі СІ одиницею коефіцієнта кінематичної в’язкості є м2с-1, в системі СГС — см2×с-1, яка має назву 1 стокс.
У даній лабораторній роботі для визначення коефіцієнта в’язкості рідини (розчин гліцерину, трансформаторне масло) застосовується метод Стокса, суть якого полягає в тому, що на кульку, яка рухається в рідині, діє сила внутрішнього тертя і гальмує її рух. Ця сила визначається за законом Стокса:
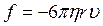 , (3)
, (3)
де r – радіус кульки,
υ – її швидкість.
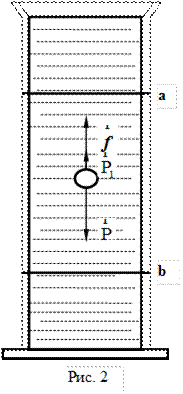
Якщо кулька вільно падає у в’язкій рідині (рис. 2), то на неї, крім сили тертя 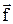 , будуть також діяти сила тяжіння
, будуть також діяти сила тяжіння 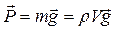 та виштовхувальна сила Архімеда
та виштовхувальна сила Архімеда 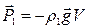 , що напрямлена вертикально вгору і рівна вазі витісненої кулькою рідини.
, що напрямлена вертикально вгору і рівна вазі витісненої кулькою рідини.
На основі другого закону Ньютона складемо рівняння руху кульки:
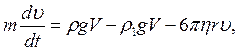 (4)
(4)
Розв’язком цього рівняння є вираз:
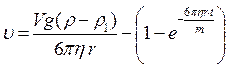 , (5)
, (5)
в чому можна переконатись безпосередньою підстановкою.
Оскільки вираз 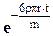 з часом дуже швидко спадає, швидкість руху кульки через малий проміжок часу встановлюється сталою і рівною
з часом дуже швидко спадає, швидкість руху кульки через малий проміжок часу встановлюється сталою і рівною
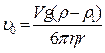 (6)
(6)
де 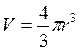 – об'єм кульки, r –густина речовини кульки, r1– густина рідини.
– об'єм кульки, r –густина речовини кульки, r1– густина рідини.
Швидкість рівномірного руху кульки можна визначити, знаючи віддаль між мітками на приладі Стокса та час, протягом якого кулька проходить цю
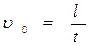 ,
,
Враховуючи вирази для υ0 та V, із співвідношення (6) знаходимо остаточну формулу для визначення коефіцієнту в’язкості:
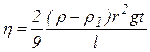
Порядок виконання роботи
1. Мікрометром виміряти діаметр d кульки.
2. Лінійкою виміряти віддаль l між гумовими мітками a і b на приладі Стокса.
3. Опустити кульку в рідину приладу і секундоміром заміряти час t її руху між мітками.
4. Ареометром визначити густину досліджуваної рідини r1, а термометром її температуру t°.
5. Повторити вимірювання відповідно п.п. 1-3 ще для двох кульок.
6. Густину матеріалу кульок r (здебільшого сталь) взяти з довідникової таблиці і дані всіх вимірювань занести в таблицю.
| № п/п | 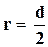 , м , м
| l, м | t, c | 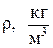
| 
| t, °C |
Обробка результатів експерименту
1. За формулою (7) знайти значення коефіцієнта в’язкості досліджуваної рідини відповідно результатів вимірювання для кожної кульки окремо.
2. Вирахувати абсолютну і відносну похибки проведеного екеперименту та оцінити його результати.
Контрольні запитання
1. Поясніть причини виникнення внутрішнього тертя.
2. Закони Ньютона та Стокса для внутрішнього тертя.
3. Поясніть фізичний зміст коефіцієнта динамічної в’язкості.
Розділ другий.
Електрика
При виконанні лабораторних робіт з електрики і магнетизму слід неухильно дотримуватись таких правил:
1. Точно виконувати вимоги внутрішнього розпорядку, встановленого в лабораторії, і суворо дотримуватись правил техніки безпеки під час роботи з електричними установками.
2. Вмикати електричну напругу і розпочинати виконання роботи лише з дозволу викладача або лаборанта після перевірки ними електричної схеми.
3. Категорично забороняється лишати без нагляду включені схеми або окремі прилади.
В лабораторних роботах з електрики і магнетизму даються посилання на слідуючі підручники:
1. Савельев И.В. Курс общей физики. Т. 2. М : Наука : 1978.
2. Яворский Б.М. и др. Курс физики. Т.2. М : Наука : 1978.
Принцип дії і основні характеристики
електровимірювальних приладів
Електровимірювальний прилад — це сукупність засобів, за допомогою яких здійснюється вимірювання певної електричної величини.
В приладах безпосередньої оцінки вимірювана величина визначається стрілочним або цифровим способом відліку, або з допомогою світлового “зайчика” на градуйованій шкалі. Це — амперметри, вольтметри, ватметри, омметри, гальванометри.
Для вимірювання електричних величин в приладах безпосередньої оцінки використовують фізичні явища, на яких створюються обертальний момент і наступне переміщення рухливої системи приладу. Обертальний момент утворюється внаслідок взаємодії постійного магніту і магнітного поля струму в котушці, магнітного поля котушки із струмом і феромагнетиком, взаємодії магнітних полів котушок з струмами, взаємодії заряджених тіл. Залежно від використовуваного в приладі принципу взаємодії розрізняють такі системи електровимірювальних приладів: магнітоелектричну, електромагнітну, електродинамічну, індукційну і ін.
Якість електровимірювальних приладів визначається чутливістю, похибками вимірювання, реагуванням на зовнішні електричні і магнітні поля та зміну температури, межами вимірювань, тривалістю щодо перевантажень тощо.
Чутливістю електровимірювальних приладів називають відношення лінійного або кутового зміщення покажчика приладу Da до зміни вимірюваної величини Dx, яка зумовила це зміщення:
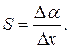
Величина С=1/S, обернена чутливості, дістала назву ціни поділки приладу.
Для характеристики точності електровимірювальних приладів використовують так звані зведені похибки;
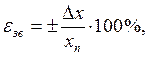
де Dx – абсолютна похибка вимірюваної величини;
xn – верхня межа вимірювань (шкали) приладу (його номінальне
значення).
Електровимірювальні прилади відповідно до величини їх зведеної похибки згідно існуючим стандартам поділяються на вісім класів точності, нанесеним на шкалу вимірювального приладу: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5. За покажчиком класу точності визначають абсолютну похибку вимірювання:
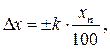
де k – клас точності приладу в процентах;
xn – максимальне значення вимірюваної величини.
Прилади класів точності 0,02; 0,05; 0,1; 0,2 використовуються, головним чином, для точних лабораторних вимірювань і називаються прецезійними; прилади класів 0,5; 1,0; 1,5; 2,5 мають назву технічних.
Прилади магнетоелектричної системи
Прилади цієї системи складаються з двох основних частин: постійного магнету і котушки, що має вигляд рамки. Принцип дії вимірювального механізму цих приладів заснований на взаємодії сильного магнетного поля постійного магнету з слабким магнетним полем рамки, по якій проходить вимірювальний струм. Схему приладу магнетоелектричної системи наведено на рис. 1.
Магнетна система вимірювального механізму складається з сильного постійного магнету 4, полюсних наконечників 5, нерухомого осердя 2.
Між полюсними наконечниками і осердям розміщується рамка (котушка) 3, що являє собою досить легкий алюмінієвий каркас, на який намотаний тонкий мідний дріт діаметром від 0,03 до 0,2 мм. Така система забезпечує вільне обертання рамки навколо осердя, а отже, і відхилення скріпленої з нею стрілки 1 відносно шкали. При проходженні струму I через рамку на неї діє обертальний момент
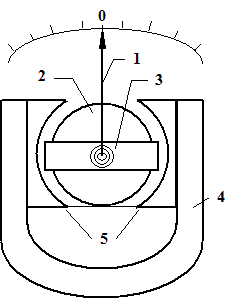
Рис. 1
M = n B S I ,
де n – кількість витків рамки;
B – магнетна індукція;
S – площа рамки.
Цей момент зрівноважується протидіючим моментом деформації спіральних пружин, які на рисунку не показані.
Прилади магнетоелектричної системи мають високу чутливість, мале споживання електричної енергії, рівномірну шкалу.
Високоточні прилади класів 0,02; 0,05; 0,1; 0,2 можуть бути лише магнетоелектричної системи.
Прилади магнетоелектричної системи мають ряд недоліків, до яких слід віднести: порівняно складна будова, чутливість до перевантажень, можливість вимірювати лише постійний струм.
Прилади електромагнетної системи
Прилади цієї системи складаються з плоскої або круглої нерухомої котушки, на яку намотаний мідний дріт, і рухомого осердя, виготовленого з м'яких магнетних матеріалів (електротехнічна сталь, пермалой). Принцип дії приладів цієї системи заснований на взаємодії магнетного поля котушки, по якій проходить струм, з рухливим феромагнетним осердям рис. 2.
Вимірюваний струм I, що проходить по котушці 3, створює магнетне поле. В це поле втягується осердя у вигляді стальної пластинки 4, закріпленої на осі 6. Намагнеченість осердя і саме магнетне поле котушки пропорційні струмові, отже, обертальний момент пропорційний квадрату струму:
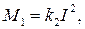
де k1 – коефіцієнт пропорційності, який залежить від конструкції приладу.
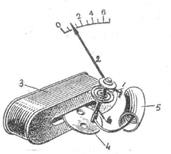
Рис. 2
Протидіючий момент M2 створюється пружинками 1. Він пропорційний кутові повороту рухливої частини приладу:
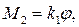
де k2 – коефіцієнт пропорційності, який залежить від пружних властивостей пружин.
Для швидкого заспокоєння рухливої частини приладу і стрілки застосовують повітряні демпфери 5. Демпфер - це камера, в якій рухається алюмінієвий поршень. При повороті осердя поршень зазнає опору повітря.
Рівновага рухливої частини приладу визначається рівністю протилежно напрямлених моментів: M1 = M2. Звідки
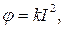
де 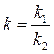 . Отже, шкала електромагнетного приладу нерівномірна, квадратична. Із зміною напряму струму змінюються як напрям магнетного поля, так і намагнеченість осердя. Отже, прилади цієї системи застосовуються для вимірювань постійного і змінного струмів. В останньому випадку вони реагують на діюче значення змінного струму, їх використовують також для вимірювання напруги в електричному колі.
. Отже, шкала електромагнетного приладу нерівномірна, квадратична. Із зміною напряму струму змінюються як напрям магнетного поля, так і намагнеченість осердя. Отже, прилади цієї системи застосовуються для вимірювань постійного і змінного струмів. В останньому випадку вони реагують на діюче значення змінного струму, їх використовують також для вимірювання напруги в електричному колі.
Недоліки приладів електромагнетної системи: нерівномірність шкали, менша точність порівняно з магнетоелектричними приладами, залежність показів від зовнішніх магнетних полів. Такого типу прилади покривають металевими кожухами, або виготовляють астатичними, тобто з двома котушками, включеними послідовно.
Прилади електродинамічної системи
Прилади цієї системи відзначаються тим, що їх дія грунтується на взаємодії магнетних полів двох котушок (рухомої і нерухомої) із вимірюваним струмом. Одна із взаємодіючих котушок нерухома і складається з двох послідовно з’єднаних котушок 4, між якими є зазор. В ньому розміщується вісь обертання рухомої безкаркасної котушки 3. З віссю скріплена стрілка 1 - покажчик з алюмінієвою пластинкою повітряного демпфера 2. Рис. 3.
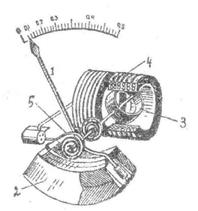
Рис. 3
На вісі також ізольовано закріплені кінці двох спіральних пружин 5, які призначені для підведення вимірювального струму і створення протидіючого моменту. Власне магнітне поле котушок мале, тому для захисту їх від впливу зовнішніх полів застосовують екранування або прилади виготовляють астатичними.
Котушки в приладах електродинамічної системи залежно від призначення їх з’єднуються послідовно або паралельно. Якщо котушки приладу з’єднати паралельно, то його можна використовувати як амперметр. Якщо обидві котушки з’єднати послідовно і приєднати до них додатковий опір, то прилад може використовуватись як вольтметр. У ватметрах нерухома котушка вмикається в коло струму послідовно, а рухома котушка з додатковим опором – паралельно споживачам енергії.
Прилади індукційної системи
Прилади індукційної системи характеризуються тим, що принцип їхньої дії грунтується на взаємодії вихрових індукційних струмів в рухомій частині приладу (алюмінієвий диск, насаджений на вертикальну вісь) із змінними магнетними потоками нерухомих електромагнетів. Один із електромагнітів має обмотку з тонкого ізольованого дроту, яка є обмоткою напруги і включається в коло паралельно навантаженню.
Серед приладів індукційної системи широке застосування мають лічильники електричної енергії змінного струму.
Прилади електронної системи
До приладів електронної системи відносяться електронні вольтметри, які складаються з електронних ламп або напівпровідникових приладів і вимірювального механізму магнетоелектричної або електростатичної системи. Прилади електронної системи використовуються для радіотехнічних вимірювань напруг і частот в значних діапазонах. Такі прилади мають досить великі вхідні опори, тому їх використовують для вимірювання напруги високоомних малопотужних джерел.
Цифрові прилади
Прилади цієї системи визначають невідому величину, що вимірюється в дискретно цифровій формі за допомогою цифрових індикаторів.
Цифрові прилади мають ряд переваг над звичайними, основні з яких: висока точність і швидкість вимірювання, об’єктивність і повна автоматизація процесу вимірювання, можливість передачі результатів на відстані і подальшої їх обробки на ЕОМ.
Поряд з перевагами цифрові прилади мають ряд недоліків; складність схеми, значні габарити, менша надійність.
 Умовні позначення на шкалах електровимірювальних приладів
Умовні позначення на шкалах електровимірювальних приладів
1. - магнетоелектрична система з рухомою рамкою;

2. - магнетоелектрична система з рухомим магнітом;

 3. - електромагнетна система;
3. - електромагнетна система;
4. - електродинамічна система;

4. - індукційна система;
 5. - електронна система;
5. - електронна система;
 6. - для постійного струму чи напруги;
6. - для постійного струму чи напруги;

 7. - для змінного струму чи напруги;
7. - для змінного струму чи напруги;
 8. - для постійного або змінного струму чи напруги;
8. - для постійного або змінного струму чи напруги;

9. - клас точності приладу;
 10. - магнетний екран;
10. - магнетний екран;
 11. - горизонтальне розміщення;
11. - горизонтальне розміщення;

12. - вертикальне розміщення;

13. - випробувальна напруга ізоляції 2 кВ.
Для правильної і ефективної організації електричних вимірювань слід перед усім докладно ознайомитися з основними характеристиками електровимірювальних приладів на їхніх шкалах.
Довільний електровимірювальний прилад у процесі вимірювань не повинен змінювати своїх параметрів і режиму дій об’єкта вимірювання. Отже, опір амперметра мусить бути по можливості малим, а опір вольтметра - великим. Розширення меж вимірювання амперметрів досягається включенням паралельно амперметру шунта. Розрахунки шунта виконують за формулою:
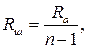
де 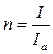 , тобто I – найбільше значення струму, який повинен вимірювати амперметр; Ia – сила струму повного відхилення стрілки (граничний струм приладу);
, тобто I – найбільше значення струму, який повинен вимірювати амперметр; Ia – сила струму повного відхилення стрілки (граничний струм приладу);
Ra – внутрішній опір приладу;
Rш – опір шунта;
Розширення меж вимірювання вольтметрів досягається включенням послідовно до вольтметра додаткового резистора Rд. Розрахунок опору додаткового резистора виконують згідно формули:
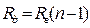 ,
,
де 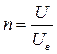 тобто U –найбільше значення напруги, яку слід вимірювати; Uв –напруга, на яку розрахований вольтметр;
тобто U –найбільше значення напруги, яку слід вимірювати; Uв –напруга, на яку розрахований вольтметр;
Rв – опір вольтметра;
Rд – додатковий опір.
Лабораторна робота №2-1
Дослідження електричного поля методом моделювання
л.1. §§ 5, 6, 13.2. §§ 2.1, 2.2, 2.3
Мета роботи: дослідити конфігурацію електростатичного поля; побудувати еквіпотенціальні поверхні і лінії напруженості для заданої форми електродів; набути навики використання теореми Гаусса.
Прилади і обладнання: мікроамперметр; вольтметр; джерело струмів.
Теоретичні відомості
Електричне поле в діелектрику подібне до поля постійного струму в провідному середовищі при однаковій конфігурації електродів. Якщо потенціали електродів в обох випадках одні і ті ж, розподіл потенціалу в діелектрику такий же, як і в провідному середовищі з струмом. Подібність полів видно із слідуючого співставлення їх властивостей.
Електростатичне поле в діелектрику потенціальне, циркуляція вектора напруженості електростатичного поля вздовж замкнутого контуру
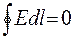 .
.
Поле в провідному однорідному середовищі /без джерел сторонніх сил/ також потенціальне. Постійний струм не створює завихрень між електродами. Тому
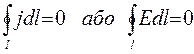
оскільки у відповідності з законом Ома
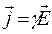 ,
,
де 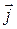 – густина струму;
– густина струму;
g – електропровідність середовища.
Існує також подібність і між граничними умовами. На границі поділу діелектриків тангенціальна і нормальна складові вектора напруженості електростатичного поля задовольняють слідуючі умови:
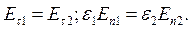
У провідному середовищі неперервність тангенціальних складових витікає із потенціальності поля струму. Граничні умови для нормальних складових вектора густини струму
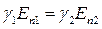
випливають із умови неперервності 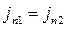 .
.
Із подібності граничних умов слідує, що провідне середовище з струмом може служити моделлю для дослідження електростатичного поля, якщо електропровідність g середовища замінити діелектричною проник-ністю e, яка задається для модельованого діелектрика, а електроди в обох випадках розмістити однаково. Поле в неоднорідному діелектрику, різні області якого мають неоднакову діелектричну проникність e, також можна моделювати на провідному середовищі, якщо подібний розподіл e і g.
Виміряти розподіл потенціалів у провідному середовищі значно простіше, ніж в діелектрику, тому дослідження на моделі має перевагу над електростатичним оригіналом. За допомогою моделювання легко визначити ємність досліджуваної системи. Розрахункова формула для ємності буде одержана, якщо в формулі
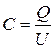
заряд замінити за теоремою Гаусса потоком вектора електростатичного зміщення через замкнуту поверхню
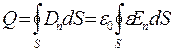
Тоді ємність
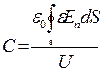 . (1)
. (1)
Потік розраховується крізь замкнуту еквіпотенціальну поверхню, яка оточує електрод модельованої системи, з використанням знайдених на провідній моделі значень нормальної компоненти вектора напруженості En. Різницю потенціалів U беруть рівною напрузі між електродами моделі, діелектричну проникливість – значенню, яке задається для модельованого діелектрика.
Досліджувальна установка
Як провідне середовище для моделі використовують провідний папір, властивості якого в площині однакові. Можна також використати воду, слабкі кислотні або лужні розчини, які наливають у плоскі ванночки розміром 10´40´40 см із хорошого діелектрика.
Моделюють плоскі поля, тобто такі, потенціал і напруженість яких залежить лише від двох координат. Плоским являється поле в циліндричному конденсаторі далеко від його кінців, в двохпровідній довгій лінії, між окремим провідником і провідною поверхнею і т.д. На провідному папері відтворюється переріз такого поля площиною, перпендикулярною до електродів.
Електрична схема досліджуваної установки подана на рис.1. Потенціал у різних точках аркуша провідного паперу 1 вимірюють з допомогою зонда 2, з’єднаного через мікроамперметр з рухомим контактом потенціометра R.
Чотири ділянки кола — дві, між рухомим контактом потенціометра і його кінцевими контактами і дві між зондом і електродами на аркуші паперу — створюють місток постійного струму. Струм у діагоналі містка дорівнює нулю, коли зонд розміщують у точці, потенціал якої співпадає з потенціалом рухомого контакту потенціометра .
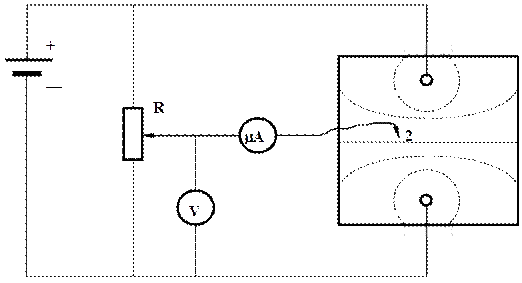
Рис. 1
Різницю потенціалів між нижнім контактом потенціометра і його рухомим контактом вимірюють за допомогою вольтметра V. До-сліджувальна установка комплектується пантографом, з допомогою якого координати зонда переносять на аркуш паперу.
В результаті вимірювань одержують картину проекцій еквіпотенціальних поверхонь на аркуш провідного паперу з заданим кроком Dj . Подібний вигляд має картина поля, яка може бути одержана при моделюванні поля двохпровідної лінії, що показана на рис.1 (штрихові лінії).
Для побудови ліній напруженості (силових ліній) використовують слідуючий спосіб (рис. 2). Проводять лінію, яка сполучує електроди, так, щоб вона співпала з віссю симетрії поля.
Із точки 0 на поверхні електрода вимірюють віддаль 01 до найближчої еквіпотенціальної поверхні. Цю віддаль відкладають вздовж поверхні електрода, одержують таким чином точку 1 на електроді. Через точку 1¢ проводять відрізок 1¢2 перпендикулярно поверхні електрода. Потім віддаль 1¢2 відкладають вздовж поверхні електрода і одержують таким чином точку 2 і т.д. Аналогічну побудову здійснюють від точки 0 в другу сторону (кожну побудову слід закінчити таким чином, щоб довжина останнього до осі симетрії відрізка на поверхні електрода була більшою довжини передостаннього). Розділивши таким чином найближчу до електрода еквіпотенціальну поверхню, через одержані точки (1; 2; 3; ... i) проводять перпендикулярні їй відрізки до перетину з слідуючою еквіпотенціальною поверхнею. Після того, як всі еквіпотенціальні поверхні будуть поділені, одержані точки слід з’єднати плавними лініями, додержуючись їх ортогональності до еквіпотенціальних ліній у точках перетину. (Якщо поле має дві осі симетрії, наприклад поле двохпровідної лінії, то побудову силових ліній слід проводити зразу від обох електродів).
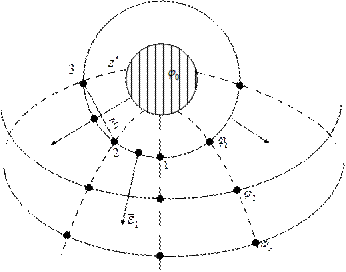
Рис. 2
Для розрахунку потоку вектора напруженості слід мати на увазі, що найближча до електрода замкнута еквіпотенціальна поверхня є деформованим циліндром, твірна якого перпендикулярна площині карти. Так як напруженість поля Ei в границях кожного відрізка еквіпотенціальної поверхні приблизно однакова, можна розрахувати елемент потоку вектора напруженості
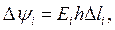 (2)
(2)
де h – висота циліндра;
Dli – довжина відрізка еквіпотенціальної поверхні (береться з карти).
Напруженість Е і розраховують за формулою
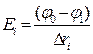 (3)
(3)
Dri визначається з карти поля як віддаль між середніми точками відрізків на поверхні електрода і на найближчій еквіпотенціальній поверхні; j0і j1— значення потенціалів на електроді і на еквіпотенціальній поверхні. Заряд, який розміщений в середині замкнутої еквіпотенціальної поверхні (циліндра), розраховують за теоремою Гаусса:
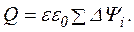 (4)
(4)
Із останньої формули легко розрахувати ємність одиничної довжини модельованої системи:
Дата добавления: 2015-10-09; просмотров: 851;
