Лабораторна робота № 1-9 2 страница

деD_о– діаметр осі маятника.

Ролик являє собою диск з отвором, тому його момент інерції вираховується за формулою:

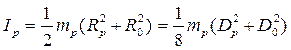, (13)

де D_p – зовнішній діаметр ролика.

Змінне кільце, як і ролик, теж диск з отвором, тому:

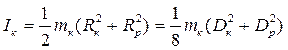(14)

де D_к–зовнішній діаметр кільця.

Таким чином, момент інерції маятника Максвелла, визначений експериментально та вирахований теоретично може служити основою дослідження справедливості закону збереження механічної енергії в умовах виконання лабораторної роботи.

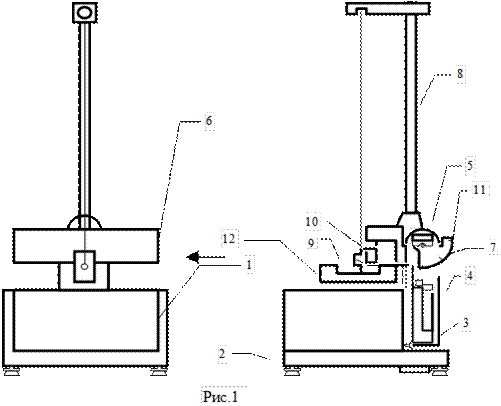
Ця лабораторна робота виконується на приладі, загальний вигляд якого зображений на рис.1. До основи приладу прикріплена колонка 1 з верхнім нерухомим 2 та нижнім рухомим 3 кронштейнами. На верхньому кронштейні знаходиться електромагніт 4, фотоелектричний датчик 5 та корбочка 6 для закріплення і регулювання довжини біфілярного підвісу маятника.

Маятник 7 — це ролик, закріплений на осі і підвішений біфілярним способом, на нього накладаються змінні кільця 8, що змінюють момент інерції системи.

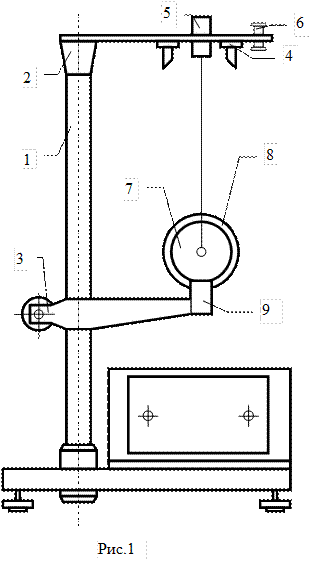
В верхньому положенні маятник утримується електро-магнітом. Довжина його визна-чається за міліметровою шкалою на колонці приладу. Для під-вищення точності вимірювань нижній кронштейн має червоний покажчик, що розташований на висоті оптичної осі нижнього фотоелектричного датчика.

Порядок виконання роботи:

1. Нижній кронштейн приладу зафіксувати в крайньому ниж-ньому положенні.

2. На ролик маятника накласти довільно вибране кільце.

3. Пересвідчитись, що край кільця при опусканні маятника перетинає оптичну вісь нижнього фотоелек-тричного датчика.

4. Натиснути клавішу "Пуск".

5. Намотати нитку підвісу на вісь маятника і зафіксувати його з допомогою електромагніта.

6. Повернути маятник в напрямку його руху на кут близько 5⁰.

7. Натиснути клавішу "Сброс".

8. Натиснути клавішу "Пуск" і записати виміряний час падіння маятника.

9. Дослід повторити 5 разів.

10. З допомогою шкали на колонці приладу визначити довжину маятника .

11. Записати маси всіх елементів маятника: осі, ролика, кільця.

12.Виконати заміри діаметрів осі маятника, нитки, ролика і кільця.

13.Дані всіх вимірювань занести в таблицю:

Обробка результатів експерименту та їх аналіз

1. Визначити середнє значення часу падіння маятника за формулою

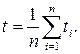
2. Використовуючи формулу (10) визначити момент інерції маятника за даними експерименту.

3. За формулою (11) визначити момент інерції цього ж маятника теоретичним способом.

4. Визначити абсолютну і відносну похибки.

5. Проаналізувати одержані результати роботи та зробити висновки.

Контрольні запитання

1. Сформулюйте закон збереження та перетворення механічної енергії.

2. Що таке момент інерції та від чого він залежить?

3. В чому полягає теорема Штейнера?

4. Доведіть вірність теореми Штейнера для стержня, використавши дані з таблиці.

5. Запропонуйте метод визначення втрат механічної енергії маятника Максвелла протягом одного періоду,

Лабораторна робота № 1-12

Визначення кінематичних характеристик гіроскопа

л.1.§§ 33,34,35

Мета роботи: поглиблене вивчення понять моменту сили та моменту імпульсу; практичне визначення кутової швидкості прецесії, моменту імпульсу і моменту інерції.

Прилади і матеріали: гіроскопічна установка з мілісекундоміром та тахометром; переміщуване тіло.

Теоретичні відомості

Слово "гіроскоп" із грецької мови означає буквально прилад для виявлення обертання. Гіроскопом називається тверде тіло, що швидко обертається, вісь обертання якого може змінювати свій напрямок в просторі.

Найбільше значення в науці і техніці мають симетричні гіроскопи. Симетричним називають гіроскоп, що має симетрію обертання відносно певної осі, яка називається геометричною віссю або віссю фігури гіроскопа. Здебільшого одна з точок осі фігури гіроскопа закріплюється і називається точкою опори гіроскопа.

Щоб вісь фігури гіроскопа могла вільно повертатися в просторі, гіроскоп закріплюється в так званому кардановому підвісі (рис. 1).

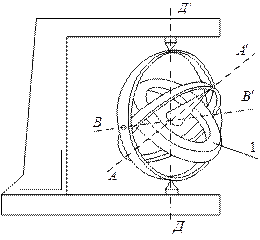
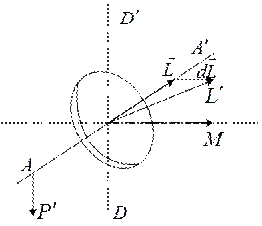
Рис.1 Рис.2

Маховик гіроскопа 1 закріплюється на осі фігури АА¢ , що може обертатись з малим тертям в підшипниках, які утримують кінці діаметра внутрішнього кільця. Внутрішнє кільце, в свою чергу, може обертатись навколо перпендикулярної осі ВВ¢ , яка проходить через підшипники на кінцях діаметра зовнішнього кільця. Нарешті, зовнішнє кільце може здійснювати рух навколо третьої осі ДД¢, що проходить через нерухомі підшипники підставки. Всі три осі перетинаються в одній точці, яка називається центром карданового підвісу. Гіроскоп у кардановому підвісі має три ступені вільності і може здійснювати любі повороти навколо центра підвісу. В елементарній теорії гіроскопа кінетична енергія та моменти імпульсу кілець не враховуються, як дуже малі в порівнянні з відповідними величинами маховика гіроскопа. Якщо центр карданового підвісу або точка опори співпадає з центром мас гіроскопа, то його називають зрівноваженим чи астатичним.

Гіроскоп має цікаві властивості, наприклад, має здатність чинити опір зовнішнім діям, що намагаються змінити напрямок його осі обертання. Якщо вдарити по кільцю карданового підвісу, то можна помітити, що гіроскоп практично не піддається дії цього удару, його вісь майже не змінює попереднього напрямку. У результаті удару виникають лише незначні коливання або дрижання осі гіроскопа, які швидко затухають. Ця властивість гіроскопа використовується в приладах орієнтації, та навігації авіаційних і космічних літальних апаратів, суден, підводних човнів та інших рухомих об’єктів. Слід звернути увагу, що така стійкість властива лише гіроскопам з трьома ступенями вільності, вона зовсім зникає, якщо гіроскоп позбавити хоч би однієї ступені вільності.

Ще одна властивість гіроскопа проявляється, коли на його вісь починає діяти сила чи пара сил, які намагаються привести вісь у рух. Під дією сили Р (рис.2) кінецьА осі АА¢ гіроскопа буде відхилятися не в бік дії сили Р, а в напрямку, перпендикулярному цій силі. У результаті гіроскоп повернеться не навколо осі ВВ¢, а навколо осі ДД¢, причому не прискорено, а з постійною кутовою швидкістю. Це обертання називають прецесією. Звідси випливає висновок, що внаслідок прецесії гіроскоп розвиває певний момент, який зрівноважує повертаючий момент сили тяжіння. Виникнення гіроскопічного моменту,зв'язаного з прецесією гіроскопа носить назву гіроскопічного ефекту.

Властивості гіроскопа притаманні також елементарним частинкам, атомам та молекулам завдяки наявності в них моментів імпульсу орбітального і спінового обертання. Звичайно, ці та інші явища мікросвіту повинні розглядатись на основі законів квантової механіки, але між властивостями атомних і макроскопічних систем є багато спільного. Тому теорія гіроскопа виявляється корисною і при вивченні атомної фізики, фізики елементарних частинок і атомного ядра.

Розглянемо рух твердого тіла, що має одну закріплену точку. Основною характеристикою дії сили на таке тіло є момент сили -це векторний добуток радіус-вектора точки прикладання сили на вектор сили:

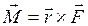. (1)

Запишемо другий закон Ньютона для поступального руху:

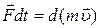. (2)

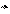Домножимо векторно це рівняння, на радіус-вектор r:

.

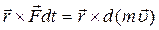або: 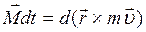. (3)

Вектор

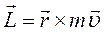, (4)

називають моментом імпульсу точки відносно вибраного початку координат. Тому вираз (3) запишемо в вигляді:

,

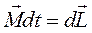або 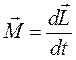. (5)

Співвідношення (5) є основним законом динаміки обертового руху тіла з однією закріпленою точкою. Він формулюється так: швидкість зміни моменту імпульсу абсолютно твердого тіла за величиною та напрямком рівна сумі моментів сил, які діють на тіло.

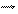Теорія гіроскопа базується на рівнянні (5). Якщо момент зовнішніх сил Мрівний нулеві, то гіроскоп називається вільним. Для вільного гіроскопа

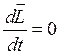,(6)

а це значить, що

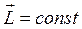(7)

Це рівняння виражає закон збереження моменту імпульсу вільного гіроскопа.

Розглянемо тепер рух гіроскопа, коли в якійсь точці А осі фігури гіроскопа АА¢ підвісити невеликий вантажР.

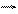У цьому випадку на гіроскоп почне діяти момент сили М, що напрямлений вздовж осі ВВ¢ (рис. 2 ) і рівний

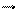
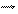M = P ´ l . (8)

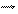
деl – плече сили Р.

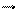Протягом часуdt момент імпульсу гіроскопа одержує прирістdL= Mdt

якийза напрямком співпадає з моментом сили М.

Тепер момент імпульсу гіроскопа буде дорівнювати результуючому вектору, L¢=L+dL , що лежить у площині, перпендикулярній площині рисунка (рис. 2 ). Напрямок цього вектора співпадає з новим напрямком осі гіроскопа, тобто, вісь гіроскопа протягом часуdt повернеться на кутdj. З рис. 2 видно, що

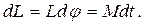(9)

Звідси можна знайти кутову швидкість повертання осі гіроскопа:

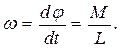(10)

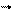
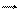
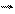Одержана формула виражає зв'язок кутової швидкості прецесії w гіроскопа з моментом зовнішніх сил, які діють на нього, та з моментом імпульсу гіроскопа. Звернемо увагу, що векториМ , l i wвзаємно перпендикулярні.

Позначимо кутову швидкість обертання гіроскопа відносно осі АА¢ через W, а його момент інерції через I, тоді останню формулу можна переписати так:

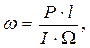(11)

звідки видно, що кутова швидкість прецесії гіроскопа обернено пропорційна кутовій швидкості обертання маховика гіроскопа.

Характерною особливістю прецесії гіроскопа є те, що вонабезінерційна, тобто прецесійний рух припиняється в момент припинення дії моменту сил. Тому поведінка прецесії подібна не швидкості, а прискоренню, так як прискорення теж припиняється одночасно з припиненням дії сили.

Слід підкреслити, що формули (10) та (11) справджуються при виконанні умовиw<< W. У техніці застосовують гіроскопи з частотою обертанняW=20000 ¸ 50000 обертів за хвилину, а величина w у мільйони разів менша.

Необхідно звернути увагу, що тут ми розглянули наближену теорію гіроскопа. Згідно із строгою теорією поряд з прецесією гіроскопа відбуваються коливання осі гіроскопа в вертикальній площині, які носять назву нутації. Із збільшенням частоти обертання гіроскопа амплітуда нутацій зменшується. Крім цього нутація гаситься тертям в опорах, тому в даній роботі вона не враховувалась.

Теорія гіроскопа сьогодні являє собою важливий розділ теоретичної механіки, який інтенсивно розвивається і є теоретичною основою найважливішої галузі сучасного приладобудування. Основи прикладної теорії гіроскопа розвинені в працях великої кількості видатних вітчизняних та закордонних вчених – М.Є.Жуковського, О.М.Крилова, Б.В.Булгакова, Г.Клейна, А.Зоммерфельда, М.Мулера та інших. Сучасний розвиток прикладна теорія гіроскопа одержала в роботах А.Ю.Ішлінського, Я.Н.Ройтенберга, В.І.Кошлякова, В.І.Назарова, М.А.Павловського та інших.

Опис лабораторної установки

Гіроскоп, що використовується в даній роботі, являє собою масивний диск, закріплений на роторі електродвигуна, На підставці з чотирма гвинтовими ніжками закріплена колонка з кронштейном, на якому розміщені фотоелектричний датчик та зовнішня втулка поворотного з’єднувача.

Поворотний з’єднувач дає можливість гіроскопу повертатись навколо вертикальної осі та забезпечує живлення струмом фотоелектричного датчика і електричного двигуна.

Електричний двигун змонтований на кронштейні таким чином, щоб була можливість повороту на обмежений кут в вертикальній площині.

На валу двигуна закріплений диск з екраном захисту. З корпусом двигуна з’єднаний важіль, з метричною шкалою, вздовж якої може переміщуватись вантаж для зрівноваження гіроскопа.

Кут повороту гіроскопа навколо вертикальної осі можна виміряти з допомогою лічильника, розташованого на передній панелі приладу. Диск має на ободі отвори для визначення частоти обертання вала електродвигуна фотоелектричним датчиком.

Порядок виконання роботи

1. Ввімкнути прилад в електричну мережу.

2. Натиснути клавішу "Сеть" і переконатись, чи всі індикатори висвічують цифру нуль та чи світяться лампочки фотоелектричних датчиків.

3. Повертаючи ручку потенціометра "Рег.скорости" переконатись, що двигун працює і стрілка вимірювача частоти обертання його вала відхиляється.

4. З допомогою переміщування вантажу встановити важіль гіроскопа горизонтально.

5. Ввімкнути двигун і встановити частоту обертання його вала біля 6000 об/хв.

6. Змістити вантаж на 2 см вліво чи вправо.

7. Натиснути клавішу "Сброс" і після повороту гіроскопа не менше, як на 30⁰, натиснути клавішу "Стоп".

8. Записати покази лічильників кутаj і часу t, а також масу переміщуваного вантажу.

Обробка результатів вимірювань

Завдання 1. Визначення кутової швидкості прецесії гіроскопа.

1. За формулою w=j / t вирахувати кутову швидкість прецесії гіроскопа.

2. Результат співставити зі швидкістю обертання вала двигуна.

3. Знайти абсолютну та відносну похибки вимірювання кутової швидкості прецесії.

Завдання 2. Визначення моменту імпульсу гіроскопа.

1. За формулою (8) знайти результуючий момент сил, що діє на гіроскоп.

2. Виходячи з формули (10) знайти момент імпульсу L гіроскопа.

3. Визначити абсолютну та відносну похибки вимірювання моменту імпульсу гіроскопа.

Завдання 3. Визначення моменту інерції гіроскопа.

1. Знаючи момент імпульсу гіроскопа Lі частоту його обертанняW, вирахувати момент інерції гіроскопа.

2. Вирахувати момент інерції гіроскопа за формулою (11). Результати співставити.

3. Визначити абсолютну та відносну похибки знаходження моменту інерції гіроскопа.

Контрольні запитання

1. Момент сили і момент імпульсу тіла відносно точки та відносно осі.

2. Основні властивості гіроскопа і їх використання в техніці.

3. В чому полягає суть гіроскопічного ефекту?

4. Рівняння обертового руху твердого тіла. Основний закон динаміки обертового руху.

Лабораторна робота № 1-13

Визначення коефіцієнта тертя кочення

л.1.§§ 11, 12, 13, 14

Мета роботи: експериментальне вивчення основних закономірностей тертя кочення.

Прилади і матеріали: спеціальна установка; набір досліджуваних тіл.

Опис установки

Установка для вимірювань являє собою похилий маятник, зображений на рис.1. До підставки 2, що має чотири гвинтових ніжки, прикріплені мілісекундомір 1 та труба 3 з змонтованим на ній корпусом 4, з’єднаним через черв’ячну передачу з кронштейном 5, який має дві шкали 6 та 7. До кронштейна прикріплена колонка 8, на якій підвішується з допомогою нитки куля з водилкою 9, та є пристрій 10 для закріплення досліджуванихзразків.Фотоелектричний датчик 12 служить для підрахунку коливань маятника.

Теоретичні відомості

Тертя кочення обумовлюється: а) втратами на пружний гістерезис, що зв’язаний з стисненням матеріалу під дією навантаження попереду тіла, яке котиться; б) затратами роботи на деформацію матеріалу при формуванні валика попереду тіла, що котиться ; в) подолання "місточків зчеплення".

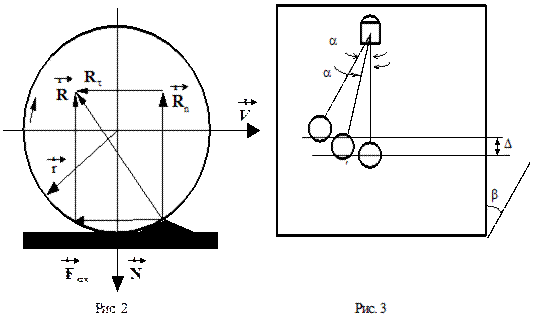
Причину виникнення тертя кочення можна проаналізувати на прикладі кочення кулі або циліндра на площині (рис. 2 ). При такому коченні в точці дотику виникають пружні або пластичні деформації. Тому точка Априкладання сили реакціїR_n поверхні дещо зміщується вперед, а лінія дії сили відхиляється від вертикалі назад.

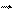Нормальна складова реакції:

,

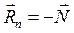а дотична тертя кочення:

.

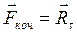У першому наближенні для сили тертя кочення виконується закон Кулона:

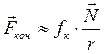, (1)

деr –радіус поверхні тіла, що котиться;

¦_к – коефіцієнт тертя кочення.

Тертя кочення значно менше, ніж тертя ковзання. При ньому набагато менше зношуються поверхні, які труться, та в багато разів знижується дисипація механічної енергії. Тому скрізь, де це можливо, тертя ковзання замінюють тертям кочення.

У всіх реальних механічних процесах та системах мають місце сили тертя, дія яких призводить в своєму результаті до перетворення енергії в тепло.

При переміщенні одного тіла відносно іншого по його поверхні виникає опір, що характеризується цілим рядом явищ, в тому числі силою тертя. Розрізняють силу зовнішнього тертя, як силу опору, тангенціальну відносно переміщення двох твердих тіл при їх дотикові і силу внутрішнього тертя як силу опору, тангенціальну відносно переміщення шарів середовища один відносно іншого.

Характерною особливістю зовнішнього тертя є наявність сил тертя спокою, що визначається як гранична тангенціальна сила, під дією якої починається відносне переміщення тіл, які дотикаються.

Основним законом для сили зовнішнього тертя є закон Амонтона-Кулона, який доповнений В.В.Дерягіним:

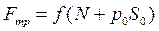, (2)

де¦ –коефіцієнт тертя ковзання;

N – нормальне навантаження;

p₀ –питома адгезія - сила прилипання, віднесена до одиниці площі;

S₀ –площа дійсного контакту.

Сила тертя визначається коефіцієнтом тертя ¦. Спостереження показують, що його величина не є сталою, а залежить від матеріалу поверхні, від їх мікрогеометричного профілю, наявності мастила, газового середовища та багатьох інших факторів.

У даній роботі коефіцієнт тертя кочення кулі по площині визначається методом похилого маятника. Куля радіусом r (рис. 3), підвішена на нитці, спирається на похилу площину, кут нахилу якої b можна змінювати. Якщо кулю вивести з положення рівноваги, вона почне перекочуватись по площині, здійснюючи затухаючі коливання під дією зовнішнього тертя.

Вимірювання сили тертя з допомогою похилого маятника грунтується на вимірюванні зменшення амплітуди його коливань протягом певної кількості циклів. Формулу для розрахунку коефіцієнту тертя можна одержати, прирівнюючи роботу сил тертя втратам потенціальної енергії маятника.

За n циклів коливань при переході з положенняВ в положення В¢ (рис. 3) маятник втрачає енергію:

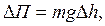(3)

деm –маса маятника ;

g – прискорення вільного падіння;

Dh – втрата висоти.

Втрата енергії рівна роботі сил опору вздовж пройденого шляхуS:

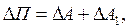(4)

деDA=F_tp ×S –робота сили тертя ; (5)

DA₁ –робота сил опору середовища та тертя в підвісі маятникa, якою в даному випадку можна знехтувати.

Таким чином:

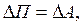(6)

Але

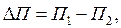(7)

де П₁– потенціальна енергія маятника в положенні В,

П₂ –потенціальна енергія маятника в положенні В¢.

З рисунка 3 видно, що

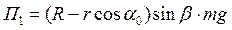, (8)

деR – довжина маятника;

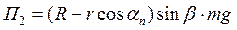. (9)

Вирази (8) і (9) підставимо в (7):

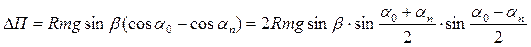, (10)

де a₀ – відхилення маятника в початковий момент часу;

a_n– відхилення маятника після n коливань.

Враховуючи, що a₀ та a_n кути малі, співвідношення (10) можна переписати:

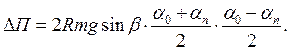(11)

З іншого боку 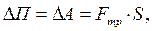де 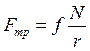–сила тертя кочення;

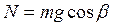– сила нормального тиску ; (12)

S –шлях, пройдений маятником заn коливань:

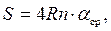(13)

де 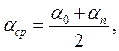тому: (14)

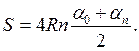(15)

Підставляючи (15) та (12) в формулу (5), знайдемо роботу:

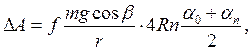
враховуючи її та (11) з формули (6) одержимо:

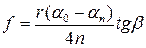, (16)

де a₀та a_n – кути відхилення першого та n-го коливань маятника в радіанах;

r –радіус кульки ;

b–кут нахилу площини коливань маятника до горизонту в градусах;

n–число повних коливань.

Отже, при умові певних наближень коефіцієнт тертя кочення між кулькою та площиною досить просто може бути виражений через експериментальне вимірювальні величини a, b, r, n.

Порядок виконання роботи

1. Вибрати кульку певного матеріалу, заміряти її радіус та закріпити на підвісі.

2. Встановити відповідну плоску пластинку.

3. Похилий маятник встановити під кутом b₁=60⁰ до горизонту.

4. Відхилити кульку на кутa₀ =4¸5⁰ від вертикалі і відпустити, даючи можливість їй здійснити n=10 (або 15 чи 20) коливань.

5. Заміряти кут a_n відхилення маятника після nколивань.

6. Всі дані занести в таблицю, виразивши кути a₀ та a_nв радіанах.

7. Повторити всі заміри для даної пари матеріалів кулька-пластинка 3¸5 разів.

8. Встановити кут нахилу площини коливань маятника за п.3 b₂ = 45⁰ і проробити вимірювання за п.п. 4¸7, потім повторити те саме при b₃ =30⁰.

Обробка результатів експерименту

1. За формулою (16) вирахувати коефіцієнт ¦ тертя кочення для кожного вимірювання фіксованих значень кута b.

2. Вирахувати середнє значення ¦ в межах серії вимірювань, тобто при кожному фіксованому значенні кута нахилу b₁, b₂, b₃.

3. Вирахувати загальне середнє значення коефіцієнта тертя кочення, абсолютну та відносну похибки експерименту.

4. Проаналізувати результати та зробити висновки про позитивні і негативні сторони даного методу вимірювання коефіцієнта тертя кочення і точність одержаних результатів.

Контрольні запитання

1. Опишіть фізичні причини, що призводять до виникнення сил тертя.

2. Запишіть та поясніть закони, які описують тертя ковзання, кочення.

3. Наведіть приклади корисного та шкідливого проявлення тертя з галузі Вашої майбутньої спеціальності.

Лабораторна робота №1-14

Визначення коефіцієнта в’язкості рідини методом Стокса

л.1.§§ 42, 43

Мета роботи: визначити коефіцієнт в’язкості досліджуваної рідини при кімнатній температурі.

Прилади і матеріали: прилад Стокса; стальні кульки; мікрометр; лінійка; секундомір; термометр.

Теоретичні відомості

Під час руху рідини між її шарами виникають сили внутрішнього тертя, які діють таким чином, щоб зрівняти швидкості всіх шарів.

Виникнення цих сил пояснюється тим, що шари, які рухаються з різними швидкостями, обмінюються молекулами. Молекули з більш швидкого шару передають більш повільному шарові певну кількість руху, внаслідок чого останній починає рухатись швидше. Молекули з більш повільного шару одержують у швидшому шарі відповідну кількість руху, що приводить до його гальмування.