Теоретическое введение. Элек­тро­ем­кость уе­ди­нен­но­го про­вод­ни­ка - это од­на из его ха­рак­те­ри­стик, ко­то­рая по­ка­зы­ва­ет

Элек­тро­ем­кость уе­ди­нен­но­го про­вод­ни­ка - это од­на из его ха­рак­те­ри­стик, ко­то­рая по­ка­зы­ва­ет, ка­кой за­ряд нуж­но со­об­щить данно­му про­вод­ни­ку, что­бы его по­тен­ци­ал из­ме­нил­ся на еди­ни­цу, и опре­де­ля­ет­ся по фор­му­ле:

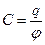, (3.1)

где C - ем­кость про­вод­ни­ка; j - потенциал, ко­то­рый по­лу­чил про­вод­ник при со­об­ще­нии ему за­ря­да q.

Элек­тро­ем­кость про­вод­ни­ка за­ви­сит от его раз­ме­ров, фор­мы, нали­чия по со­сед­ст­ву дру­гих про­вод­ни­ков и от ди­элек­три­че­ской прони­цае­мо­сти сре­ды.

Еди­ни­цей элек­тро­ем­ко­сти в сис­те­ме СИ яв­ля­ет­ся 1 фа­ра­да - это элек­тро­ем­кость та­ко­го про­вод­ни­ка, по­тен­ци­ал ко­то­ро­го при со­об­щении за­ря­да в 1 Ку­лон из­ме­ня­ет­ся на 1 Вольт.

Кон­ден­са­то­ром на­зы­ва­ет­ся со­во­куп­ность двух лю­бых проводников с оди­на­ко­вы­ми по аб­со­лют­но­му зна­че­нию, но про­ти­во­по­лож­ны­ми по зна­ку за­ря­да­ми.

Ем­кость кон­ден­са­то­ра оп­ре­де­ля­ет­ся от­но­ше­ни­ем за­ря­да на од­ной из его об­кла­док к раз­но­сти по­тен­циа­лов ме­ж­ду об­клад­ка­ми:

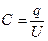. (3.2)

В боль­шин­ст­ве слу­ча­ев фор­ма об­кла­док кон­ден­са­то­ра и их вза­им­ное рас­по­ло­же­ние под­би­ра­ют та­ким об­ра­зом, что­бы внеш­ние по­ля су­ществен­но не влия­ли на элек­три­че­ское по­ле ме­ж­ду ни­ми и си­ло­вые линии, на­чи­наю­щие­ся на од­ной из об­кла­док, обя­за­тель­но за­кан­чи­ва­лись на дру­гой. Бла­го­да­ря это­му все­гда обес­пе­чи­ва­ет­ся ра­вен­ст­во аб­солют­ных зна­че­ний за­ря­дов на об­клад­ках.

К про­стей­шим ти­пам кон­ден­са­то­ров от­но­сят­ся пло­ские, сфе­ри­че­ские и ци­лин­д­ри­че­ские.

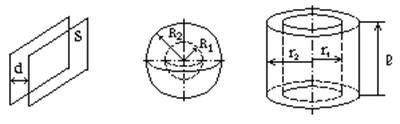Рис.3.1 Рис.3.2 Рис.3.3

Емкость приведенных на рисунках 3.1–3.2 конденсаторов может быть рассчитана по формулам:

плос­кий конденсатор (рис. 3.1):

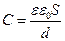; (3.3)

сфе­ри­че­ский конденсатор (рис. 3.2):

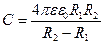; (3.4)

цилиндрический конденсатор (рис. 3.3):

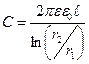(3.5)

Докажем формулу (3.4). Для вычисления разности потенциалов на обкладках конденсатора воспользуемся формулой связи напряженности электростатического поля и потенциала: 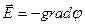; или, то же самое в интегральной форме: 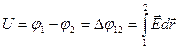. Интегрировать здесь будем по радиус-вектору, проведенному от внутренней обкладки к внешней. Вектор напряженности поля направлен радиально (в силу симметрии), тогда

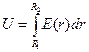. (3.6)

Напряженность поля между обкладками можно найти по теореме Остроградского-Гаусса (3.7), согласно которой поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных поверхностью, деленной наεε₀:

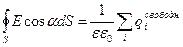. (3.7)

В качестве Гауссовой поверхности в нашем случае следует взять сферу, концентрическую обкладкам, радиусом r: R₁<r<R₂. Из-за симметрии напряженность поля в любой точке сферы одинакова и совпадает по направлению с нормалью к поверхности в данной точке, и величину Е можно вынести из под знака интеграла в (3.7), а 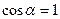. В правой части (3.7) суммарный заряд, охваченный Гауссовой поверхностью, - это заряд внутренней обкладки, то есть заряд конденсатора q. Тогда

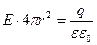. (3.8)

Здесь учтено, что 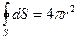- площадь сферы. Выразив Е из (3.8) и подставив в (3.6), получим:

,

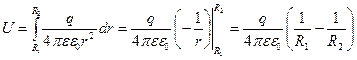откуда с учетом (3.2) получается (3.4).

Аналогично докажем (3.5). В качестве Гауссовой поверхности здесь следует взять цилиндр, коаксиальный обкладкам цилиндрического конденсатора, радиусом r: r₁<r<r₂ и длиной l. Тогда из (3.7) получим:

.

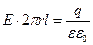Далее, из (3.6):

,

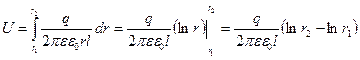Откуда с учетом (3.2) получим (3.5).

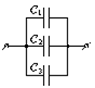Рис. 3.4

Кон­ден­са­то­ры ха­рак­те­ри­зу­ют­ся не толь­ко их элек­три­че­ской ем­ко­стью, но так­же и на­пря­же­ни­ем про­боя – та­кой ми­ни­маль­ной раз­но­стью по­тен­циа­лов об­кла­док, при ко­то­рой про­ис­хо­дит элек­три­че­ский раз­ряд че­рез слой ди­элек­три­ка в кон­ден­са­то­ре.

В тех слу­ча­ях, ко­гда ем­ко­сти од­но­го кон­ден­са­то­ра ока­зы­ва­ет­ся не­дос­та­точ­но, кон­ден­са­то­ры со­еди­ня­ют па­рал­лель­но (рис.3.4). При этом на­пря­же­ние на кон­ден­са­то­рах ока­зы­ва­ет­ся оди­на­ко­вым: U_i=U. Об­щий за­ряд ба­та­реи

,

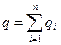где n - об­щее чис­ло кон­ден­са­то­ров; q_i - за­ряд i-го кон­ден­са­то­ра. Ем­кость ба­та­реи кон­ден­са­то­ров рав­на сум­ме ем­ко­стей от­дель­ных кон­ден­са­то­ров. С учетом того, что из (3.2) заряд каждого конденсатора q_i=C_iU_i, где С_i - емкость i-го кон­ден­са­то­ра, а общий заряд q=CU,

,

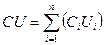и после сокращения:

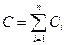(3.9)

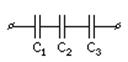Рис. 3.5

По­сле­до­ва­тель­но кон­ден­са­то­ры со­еди­ня­ют в том слу­чае, ко­гда их нужно вклю­чить в цепь с на­пря­же­ни­ем вы­ше то­го, на ко­то­рое рас­счи­тан от­дель­ный кон­ден­са­тор. При по­сле­до­ва­тель­ном со­еди­не­нии кон­ден­саторов (рис. 3.5) за­ря­ды на кон­ден­са­то­рах оди­на­ко­вы: q_i=q, а полное напряжение на батарее равно сумме напряжений:

.

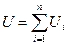С учетом (3.2) 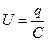, , 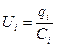тогда получим:

,

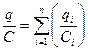и после сокращения:

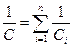, (3.10)

то есть ве­ли­чи­на, об­рат­ная ем­ко­сти ба­та­реи, рав­на сум­ме об­ратных ве­ли­чин ем­ко­стей от­дель­ных кон­ден­са­то­ров.

При по­сле­до­ва­тель­ном со­еди­не­нии за­ря­ды на кон­ден­са­то­рах оди­на­ко­вы, на­пря­же­ние на них рас­пре­де­ля­ет­ся в за­ви­си­мо­сти от их ем­ко­стей, чем умень­ша­ет воз­мож­ность про­боя кон­ден­са­то­ра.