Поняття про вектор (диполь) серця і вектор відведення

Внаслідок того, що в кожен момент часу періоду деполяризації і реполяризації серця потенціал в будь-якій точці тіла визначається сукупністю елементарних диполів, в грубому наближенні потенціал в цілому може бути описаний векторною сумою дипольних моментів окремих його частин. При цьому повністю нехтується розміщення реальних джерел в просторі, так як всі дипольні елементи джерела вважаються розташованими в одній і тій же точці. В результаті джерело зводиться до одного диполя, який називається диполем серця або вектором серця (рис. 2.11). Хоча таке наближення здається досить грубим, воно часто застосовується на практиці і дає цілком задовільні результати при моделюванні електрокардіографічних процесів.

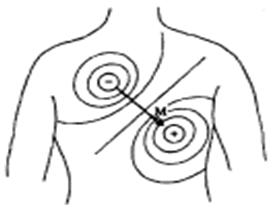
Рис. 2.11. Серцевий диполь, що складається з рівних по модулю (+) і (-) зарядів, розділених відстанню. Протягом серцевого циклу змінюється напрямок і величина векторного дипольного моменту М. Навколо М ─ еквіпотенціальні лінії серцевого диполя на піку R зубця

Враховуючи той фактор, що формування і зміна вихідних елементарних дипольних моментів мають відносно неперервний, плавний характер, можна припустити, що вектор серця буде змінюватися (по модулю і напрямку) досить плавно. Уявлення про серце як про електричний генератор з дипольною структурою є основоположним у клінічних методах інтерпретації електрокардіограми. Так, векторкардіографія повністю базується на оцінці зміни кривої, що описується кінцем вектора серця протягом серцевого циклу. Ця просторова крива називається векторною петлею. Вона має досить гладку форму. Векторкардіографічні прилади викреслюють векторну петлю в проекціях на координатні площини заданої системи координат.
В будь-який момент часу протягом процесу деполяризації або реполяризації в серці можуть існувати одна або більше незамкнутих ізохронних поверхонь збудження, і кожна така поверхня може розглядатися (принаймні наближено) як джерело у формі рівномірного дипольного шару. Елементарні диполі, що орієнтовані по нормалі до поверхні збудження, займають відносно вузьку область простору, яка відповідає товщині фронту збудження. Елементарні дипольні джерела, які розподілені таким чином в м'язі серця, можна охарактеризувати векторною щільністю дипольного моменту:

.

Тоді вектор серця 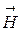пов'язаний з величиною 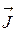наступним простим співвідношенням:

.

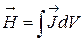"Дипольна гіпотеза" зводиться до припущення про те, що величина 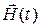дає досить точний опис сумарної активності джерел струму серця. Обгрунтованість апроксимації залежить від відношення протяжності області джерел до точки спостереження поля. Така апроксимація, очевидно, ігнорує вплив просторового розподілу реальних джерел і повинна бути недостатньо точною, проте, з її допомогою вдається отримати дуже хороші практичні результати.

Напруга між двома електродами, розташованими на поверхні тіла – напруга відведення – залежить від розташування електродів, вектора серця і характеристик грудної клітки як неоднорідного об'ємного провідника. Внаслідок того, що дана електродинамічна система, незважаючи на її складність, є лінійною, можна розділити зазначені фактори на компоненти вектора серця і всі інші фактори. Остання група включає чинники, що характеризують вплив геометричних параметрів системи та електричної неоднорідності її структури.

Якщо задати деяке конкретне розташування диполя серця (зазвичай його розміщують в геометричному центрі серця), а також розташування електродів відведення, можна розглядати вектор серця, наприклад, як дипольний момент, що орієнтований по осі Х і має одиничну абсолютну величину дипольного моменту. При цьому відведення буде вимірювати величину 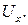Аналогічний одиничний диполь, орієнтований по осі Y, створює напругу 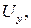а одиничний диполь, орієнтований по осі Z – напругу 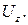Враховуючи лінійність даної системи і принцип суперпозиції, знайдемо, що для вектора

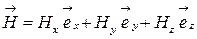
напруга відведення виражається як

.

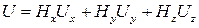Останній вираз можна трактувати як скалярний добуток вектора серця 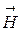і вектора 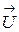з компонентами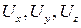

.

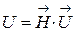Отриманий вираз показує залежність напруги відведення як від вектора серця, так і від іншого вектора, що відображає вплив геометричної структури та електричної неоднорідності середовища. Цей останній вектор називають вектором відведення.