Необхідно визначити шляхи побудови оптимальних БЕС на основі вибору правил рішень, яким відповідають екстремуми (мінімуми) середніх втрат.
В теорії рішень найбільш часто використовується дві функції втрат:
1. 
- функція втрат, в якій при зв'язку сигналів з можливими рішеннями встановлюються постійні вартості.
2. 
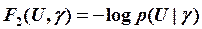- функція втрат, де p представляє ймовірність виявлення або оцінювання сигналу U.
Підстановка даних функцій у вираз для функції середніх втрат призводить до виразів, які описують якість БЕС:
1. Середню вартість втрат:
(1.3)
2.Середні втрати інформації:
(1.4)
де 
- щільність ймовірності вектора переданих сигналів U; 
- правило вибору рішень.
Розгляд проблеми оптимізації БЕС можна виконати в загальному вигляді. При цьому, в системі можуть прийматися рішення: або у вигляді «так-ні» (типові для завдань виявлення сигналів) або у вигляді вимірювань (характерні для оцінювання сигналів).
У звязку з тим, що середовище розповсюдження найчастіше некероване, то для досягнення оптимуму залишається можливість підбору оператора перетворення приймача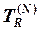 
, передавача 
, або того і другого разом:
(1.5)
Для вирішення проблеми оптимізації треба вибрати критерій оптимізації та правило вибору рішення.
1. Одним з найбільш поширених критеріїв є метод мінімізації середнього ризику або вартості 
. Величина, отримана з умови
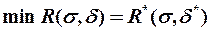(1.6)
називається мінімальним або байесовим ризиком, де 
- оптимальне правило вибору рішення.
2. Другий поширений критерій - метод мінімізації середніх втрат інформації 
. Величина, отримана з умови
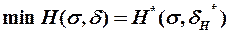(1.7)
называється мінімальною втратою інформації, где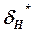 
- оптимальне правило вибору рішення.
Шляхом відповідного вибору операцій: 
або 
можна оптимальним чином вибрати правила рішення і побудувати оптимальну БЕС.
Дата добавления: 2015-10-09; просмотров: 640;