Следует различать понятия: резистор и сопротивление.

Резистор – это элемент, обладающий сопротивлением, например, кусок проволоки, катушка, реостат. Любой участок электрической цепи имеет сопротивление.

Сопротивление- это физическая величина, характеризующая способность проводника препятствовать прохождению электрического тока. На электрических схемах обозначается буквой R.

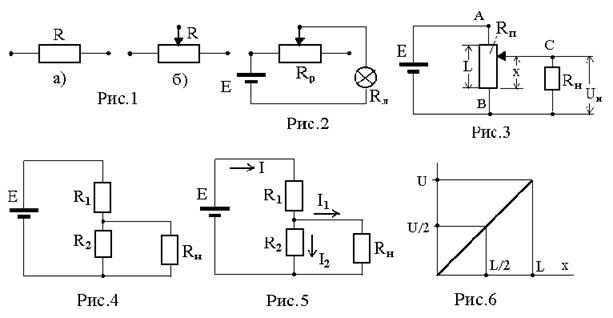
Различают резистор с постоянным сопротивлением (рис.1а) и переменный резистор (рис.1б). Конструктивно переменный резистор может быть выполнен линейным или круговым.

Примечание: большинство ручек управления радиоприёмников, телевизоров и т.п. связано с переменным сопротивлением.

Реостат и потенциометр – это схемы включения переменного сопротивления.

Включение переменного сопротивления по схеме реостата показано на рис.2. Реостат служит для изменения силы тока в цепи. В схеме на рис.2 реостатом регулируется яркость лампы с сопротивлением R_Л .

Включение переменного сопротивления по схеме потенциометра показано на рис.3. Потенциометр служит для плавного регулирования напряжения на участке цепи. Он играет роль делителя напряжения (подробнее ниже).

Следует различать «вход» и «выход» потенциометра. Клеммы «А» и «В» являются входом потенциометра, клеммы «С» и «В» (или «С» и «А») - выходом. Источник тока присоединяется к потенциометру к клеммам «А» и «В». Регулируемое напряжение U снимается со скользящего контакта «С» и одной из нижних клемм, например «В» (или «А»), к которой присоединён источник. При таком включении напряжение может изменяться от нуля до максимального значения, определяемого ЭДС источника.

В данной работе используется переменное сопротивление линейного типа. Исследуется зависимость напряжения, снимаемого с потенциометра, от длины х введенной его части при различных сопротивлениях внешней цепи (сопротивление нагрузки) R_н. На рис.3: Е – ЭДС источника питания; R_п - сопротивление потенциометра; x – длина введенной части потенциометра; L – полная длина потенциометра;

Покажем, что потенциометр является идеальным делителем входного напряжения только, если сопротивление нагрузки отсутствует (R_н =¥) или много больше сопротивления введенной части потенциометра.

Рассмотрим рис.3 и рис.4. Пусть R_н нет и скользящий контакт «С» стоит посередине, т.е. х=L/2. Тогда сопротивление потенциометра R_п можно представить состоящим из двух равных частей: R₁ и R₂ ; R_п= R₁+ R₂. Очевидно, что напряжение U на этих сопротивлениях будет делиться пополам (см. рис.6),т.е. потенциометр будет идеальным делителем.

Теперь рассмотрим как изменяется напряжение на выходе потенциометра при наличии R_н.Расчёт напряжения на этом сопротивлении можно выполнить двумя способами: с помощью законов Ома и с помощью правил (законов) Кирхгофа.

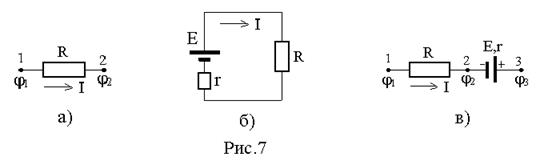
Рассмотрим первый способ. Напомним, что существует 3 вида записи закона Ома в зависимости от вида участка цепи постоянного тока. На рис.7 показаны три основных вида участков:

1. Участок, содержащий только сопротивление R, т.н. однородный участок - рис.7 а). Закон Ома для этого случая имеет вид:

I= 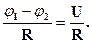(3)

2. Закон Ома для замкнутой (одноконтурной) цепи с источником тока рис.7 б):

I= 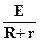или I(R+r)=Е (4)

3. Закон Ома для участка цепи, содержащей ЭДС и сопротивление R₀=R+r, т.н. неоднородный участок -рис.7 в) имеет вид:

IR₀=j₁- j₃+Е, или 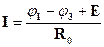(5)

Выражение (5) является наиболее общей формой закона Ома, из которой следуют два предыдущих случая.

Примечание. Участок на рис.7 в) выбран из некоторой произвольной электрической цепи. В ней могут быть другие ЭДС, не входящие в выделенный участок, под действием которых ток по данному участку может течь и навстречу данной ЭДС Е.Если ЭДС Е направлена встречно току, текущему по данному участку, то в формуле (5) ее надо взять со знаком минус. За направление ЭДС принято направление от «-» к «+» (внутри ЭДС).

Рассмотрим конкретный пример расчета напряжения на нагрузке, показывающий как изменяется напряжение на выходе потенциометра при небольших величинах R_н.

Пример. Пусть х = L/2, R_п =200 Ом, тогда R₁ = R₂ = 100 Ом, Е =10 В, R_н=10 Ом. Для расчета напряжения на нагрузке U_нвоспользуемся схемой на рис.4. Чтобы можно было использовать закон Ома в виде (4) надо преобразовать схему на рис.4 к одноконтурной. Для этого необходимо заменить параллельно соединенные сопротивления R₂и R_нодним, общим - R_o.По формуле 1/R_o=1/R₂+1/R_н, подставив численные значения, найдём R_o»9,1 Ом.

Внимание! Для самоконтроля: общее сопротивление двух параллельно соединенных сопротивлений должно быть меньше меньшего.

Далее, по формуле (4) найдем ток в контуре состоящем из источника тока с э.д.с. Е и сопротивлений R₁ и R_o :I=E /( R₁ + R_o)= 10/ (100+9,1)= 0,09 А.

Теперь найдём напряжение на нагрузке U_н : U_н=I× R_o=0,09×9,1= 0,82 В .

Обратите внимание: после подключения к потенциометру R_н=10 Ом напряжение на выходе потенциометра уменьшилось более чем в 5 раз.

Вывод: Чем меньше сопротивление нагрузки Rн(шунтирующее выходное сопротивление потенциометра), тем меньше напряжение на нагрузке. Характеристика потенциометра (зависимость выходного напряжения от длины x введенной части потенциометра) становится нелинейной. Нелинейность тем больше, чем меньше Rн.

Второй способопределения напряжения на R_н заключается в применении правил (законов) Кирхгофа. Это не сложная задача. Начало её решения показано на рис.5. Необходимо выбрать направления токов в ветвях и составить систему уравнений. Сделайте это самостоятельно. Соответствующий теоретический материал по правилам Кирхгофа можно найти в лаб. работе №204 или в учебнике Т.И.Трофимовой.