Определение удельного сопротивления проводника

Краткая теория:

(Рекомендуем вначале ознакомиться с теоретической частью работы 201а.)

В этой работе определяется удельное сопротивление нихромовой проволоки 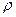, которое определяется по формуле:

, (1)

гдеR – сопротивление отрезка проволоки, l - его длина, S – площадь поперечного сечения проволоки.

Для нахождения площади поперечного сечения S измеряют микрометром диаметр проволоки d. Отсчет ее длины l производится по метрической стойке, закрепленной на стойке прибора. Для определения сопротивления проволоки по формуле 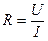(закон Ома для участка цепи), измеряют напряжение U на концах проволоки и ток I, текущий при этом через нее.

Для измерения силы тока служат амперметры, которые включают в цепь последовательно, а для измерения напряжения пользуются вольтметрами, которые включают параллельно исследуемому участку.

Различие в способах включения вольтметра и амперметра в электрическую цепь приводит к совершенно различным требованиям, которым должно удовлетворять внутреннее сопротивление этих приборов. Включение любого измерительного прибора в цепь всегда приводит к некоторому перераспределению токов и напряжений в исследуемой цепи. Желательно, чтобы это перераспределение было, по возможности, незначительным. Поэтому необходимо, чтобы амперметр обладал малым сопротивлением, а вольтметр – большим по сравнению с сопротивлением исследуемой цепи или её участка.

При изменениях тока I и напряжения U возможны два способа включения амперметра и вольтметра. Допустим, что мы используем эталонные амперметр и вольтметр, т.е. приборы, не имеющие собственных погрешностей. Но и в этом случае при обоих способах включения приборов мы будем допускать систематическую погрешность, обусловленную выбором схемы.

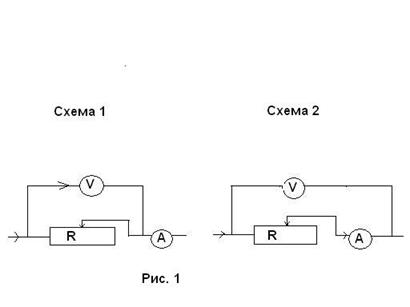
Действительно, в первой схеме на рис.1 эталонный вольтметр точно измеряет напряжение U_R тогда как эталонный амперметр измеряет суммарный ток I через вольтметр I_v и сопротивление I_R

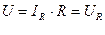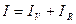, (2)

Так как 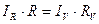, то 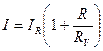, и измеренное значение сопротивления 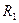для первой схемы включения амперметра и вольтметра равно:

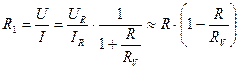(3)

Здесь 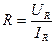- сопротивление проволоки, 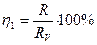-систематическая относительная погрешность при измерениях сопротивления по первой схеме (соотношение (3) справедливо при малых значениях 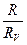). В случае использования второй схемы (см. рис.1) измеряемое вольтметром напряжение U равно:

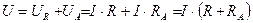(4)

Следовательно, измеренная величина сопротивления равна:

(5)

Величина 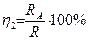- систематическая относительная погрешность при измерениях сопротивления по второй схеме.

Таким образом, чтобы добиться минимальной систематической погрешности в определении R, нужно сначала приближенно оценить величину R и затем найти значения

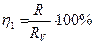и (6)

При измерениях сопротивления на практике, разумеется, лучше пользоваться той схемой, где погрешность минимальна.

Описание установки:

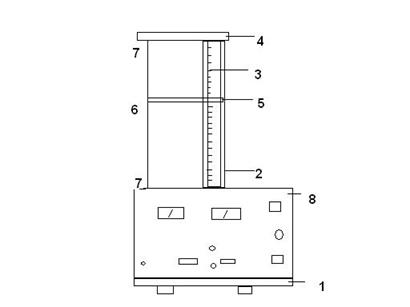
Основание 1 оснащено регулируемыми ножками, которые позволяют произвести выравнивание положения прибора. К основанию прикреплена стойка 2 с нанесенной метрической шкалой 3. На стойке смонтированы два неподвижных кронштейна 4 и один подвижный кронштейн 5, который может передвигаться вдоль стойки и фиксироваться в любом положении. Между верхним и нижним кронштейнами натянут измеряемый проводник 6, который прикреплен к кубикам 7 с помощью винтов. Через контактный зажим на подвижном кронштейне обеспечивается хорошее гальваническое соединение с измеряемым проводником. На подвижном кронштейне нанесена стрелка, которая определяет на шкале длину отрезка измеряемого проводника. Нижний, верхний и центральный контакты подведены при помощи проводов низкого сопротивления к измерительной части прибора 8, которая помещена в центральном корпусе и при помощи винтов прикреплена к основанию.

Вид лицевой панели измерительного блока представлен на рисунке: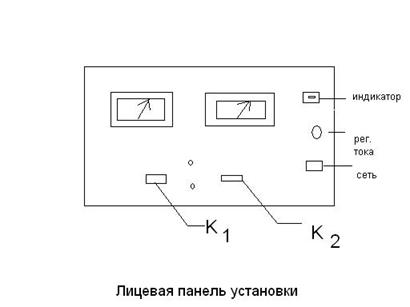

Включение прибора производится нажатием кнопки «сеть», при этом в правом верхнем углу лицевой панели начинает светиться лампочка – индикатор. Кнопка «мост» - переключатель рода работы. В ненажатом состоянии кнопка обеспечивает режим согласования прибора с мостом постоянного тока. При выполнении работы эта кнопка всегда должна быть нажата. В таком режиме прибор обеспечивает стабилизацию тока, идущего по нихромовой проволоке, т.е. при измерении длины проволоки величина идущего по ней тока будет поддерживаться постоянной. В таком режиме прибор обеспечивает стабилизацию тока, идущего по нихромовой проволоке, то есть при изменении длины включенной в сеть проволоки величина идущего по ней тока будет поддерживаться постоянной.

Кнопка служит для перехода от измерения сопротивления по схеме 1 (кнопка нажата), к схеме 2 (кнопка не нажата).

Для регулировки величины стабилизированного тока служит ручка «Рег. тока».

Измерения и обработка результатов

Техника безопасности:

- прибор допускается к эксплуатации только при наличие заземления;

- в случае каких-либо неполадок обращаться к преподавателю или лаборанту.

Измерения:

Прибор готов к измерениям непосредственно после включения напряжения цепи (кнопка «сеть») и не требует времени для прогрева.

1.Определите диаметр проволоки с помощью микрометра не менее чем в пяти точках по всей ее длине.

2.Установите подвижный кронштейн на отметку 15 см и ручкой «Рег. тока» установите по миллиамперметру ток 200 мА.

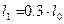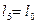3.Снимите зависимость напряжения на проволоке U от ее длины по схеме 1 (кнопка нажата). Измерения произвести для пяти значений длины проволоки l, начиная от значения , до , где 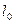- полная длина проволоки.

4.Для каждого значения 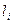- рассчитайте соответствующее значение сопротивления 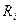по формуле:

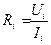(7)

5.Для значени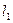й и 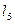рассчитайте относительную приборную погрешность по формуле:

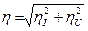, (8)

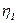где и 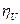- относительные погрешности вольтметра и амперметра. (Как определить относительные погрешности амперметра и вольтметра читайте во Введении к лабораторным работам.)

Для этих же значений 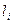рассчитайте по формуле 6 относительную погрешность , связанную с выбранной схемой измерения (внутреннее сопротивление вольтметра 2500 Ом).

Сравните полученные значения и и оцените, какой из них можно пренебречь в данном случае.

6.Для каждого значения 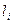рассчитайте соответствующие значения 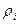по формуле (1) с учетом того, что 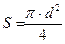. Вычислите среднее значение . Результаты занесите в таблицу:

№

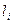
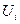
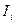
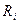
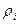
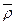
7.Снимите зависимость напряжения на проволоке от ее длины по схеме 2 (кнопка 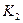не нажата). Расчеты и измерения проводятся аналогично предыдущим пунктам. Только вместо систематической погрешности рассчитывается погрешность 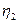по формуле (6). Внутреннее сопротивление амперметра берется равным 0.15 Ом. Результаты занести в таблицу:

№

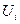
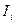
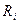
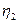
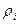
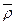
8. Для вычисленных значений сопротивления построить графики .

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Характеристики электростатического поля.

Всякий заряд изменяет свойства пространства вокруг себя - со­здает электромагнитное поле. Вокруг покоящегося заряда существует электростатическое поле. Оно характеризуется вектором напряженнос­ти 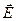и потенциалом 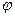. Вектор 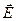является силовой характеристикой электрического поля и определяется как отношение силы 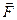действующей на некоторый "пробный" (точечный) заряд 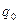, помещен­ный в данную точку пространства, к величине этого заряда:

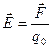
Потенциал 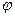электрического поля является энергетической характеристикой и определяется как отношение потенциальной энергии W, которой обладает точечный заряд, помещенный в данную точку пространства, к величине этого заряда:

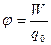
И напряженность поля и потенциал характеризуют только поле, и не зависят от величины пробного заряда. Проекция 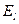вектора напряженности 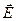на произвольную ось l и потенциал φ связаны соотношением:

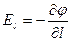
или в векторной форме

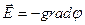
Отсюда

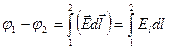
Таким образом, если известна одна характеристика поля ( 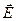или φ), то можно найти и другую (φ или ).

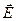Для графического изображения электростатических полей исполь­зуются силовые линии и эквипотенциальные поверхности. Силовые ли­нии проводятся таким образом, чтобы выполнялись следующие условия:

1. Направление касательной к силовой линии в каждой точке пространства совпадает с направлением вектора 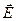в этой точке.

2. Число силовых линий, проходящих через перпендикулярную к ним площадку единичной площади, пропорционально модулю вектора напря­женности.

Силовые линии электрического поля незамкнуты. Они начинаются и заканчивается на зарядах или в бесконечности. В силу однозначного направления вектора напряженности в каждой точке поля силовые ли­нии нигде не пересекаются.

Эквипотенциальная поверхность - это поверхность, все точки который имеет одинаковый потенциал. Вектор 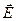перпендикулярен, к экви­потенциальной поверхности в любой ее точке и направлен в сторону уменьшения потенциала.

Основной задачей электростатики является нахождение напряжен­ности и потенциала. Опыт показывает, что напряженность поля, созда­ваемого системой N точечных зарядов, равна векторной сумме напряженностей, создаваемых каждым из зарядов в отдельности:

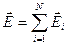
Это утверждение носит название принципа суперпозиции электрических полей.

Потенциал результирующего поля, образованного системой из N точечных зарядов, определяется путем алгебраического суммирования потенциалов:

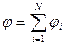
Принцип суперпозиции позволяет достаточно просто определить напряженность поля лишь для небольшого числа точечных зарядов. В более сложных случаях, в частности, для заряженных тел, облада­ющих симметрией (плоскость, цилиндр, шар и т.д.), напряженность поля может быть найдена с помощью теоремы Гаусса:

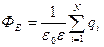
Поток вектора напряженности через некоторую замкнутую поверхность S пропорционален сумме зарядов, находя­щихся в объеме, ограниченном данной поверхностью. Символ 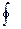означает интеграл по замкнутой поверхности S; -нормаль­ная составляющая Е для элементов интегрирования .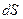

Аналитический расчет поля заряженного тела произвольной формы представляет собой непростую задачу, поэтому электростатические поля сложной конфигурации исследуются экспериментально.

Моделирование электростатического поля (метод электролитической ванны)

Одним из методов исследования в физике является модельный эксперимент, который имеет две разновидности - физическое и мате­матическое моделирование. В процессе физического моделирования наиболее существенные закономерности в поведении исследуемого объ­екта воспроизводятся па модели, сохраняя при этом свою физическую природу. В основе математического моделирования лежит тождествен­ность математического описания различных по своей природе физичес­ких явлений.

Известно, что потенциалы электростатического поля в вакууме и поля тока в электролите удовлетворяют одному и тому же виду диф­ференциального уравнения. Граничные условия для зарядов на поверх­ности проводника в вакууме и для токов в проводящей среде с малой проводимостью также совпадают. Это обстоятельство позволяет исполь­зовать электролитическую ванну для моделирования электростатичес­кого поля, поскольку проведение непосредственных электростатических измерений представляет технически достаточно сложную задачу.

Для определения поля заряженных проводников заданной формы их помещают в ванну, заполненную слабопроводящей жидкостью, и по­дают на них потенциалы, равные натуральным или уменьшенные. Следует отметить, что работа электростатического поля при перемещении за­ряда определяется разностью потенциалов 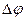, поэтому в лабора­торной работе определяется величина 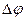, а не абсолютные значе­ния потенциалов.

Напряжением U на данном участке цепи называется величина, равная суммарной работе электростатических и сторонних сил при пе­ремещении единичного положительного заряда. При отсутствии источ­ников тока напряжение на участке цепи совпадает с разностью потен­циалов, т.е. Δφ=U=JR.

В настоящей работе экспериментально изучается распределение потенциала в пространстве между электродами, где Δφ=U, а силовые линии изучаемого поля строятся как ортогональные к найденным экспериментально линиям равного потенциала.