Формула включений-исключений

Из правила сложения с применением других теоретико-множественных операций может быть выведена формула включений-исключений (или принцип (правило) включений-исключений). Это правило позволяет рассчитать количество элементов в объединении конечных множеств, которые в общем случае могут пересекаться друг с другом. При двух множествах A и B (рис. 5.2) правило имеет вид:

N(AÈB) = N(A) + N(B) – N(AÇB),
где N(A), N(B), N(AÈB), N(AÇB) – числа элементов в исходных множествах А и В, их объединении AÈB и пересечении AÇB.

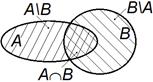
Рис. 5.2. Объединение двух множеств A и B

Поскольку вывод данной формулы требует применения дополнительных теоретико-множественных операций разбиения множества на разность и пересечение, то правило включений-исключений нельзя вывести из правила сложения средствами самой теории (комбинаторики). Для сведения правила включений-исключений к параллельной схеме расчета в формуле необходимо использовать разности множеств (рис. 5.2):

N(AÈB) = N(A\B) + N(B\A) + N(AÇB),
где A\B – результат вычитания множества B из множества A, B\A – результат вычитания множества A из множества B.

В полученной формуле комбинаторным правилом является объединение, а операции вычитания и пересечения играют вспомогательную роль. При этом расчетная схема принимает стандартный для параллельных вычислений вид (рис. 5.3):

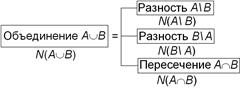
Рис.5.3. Расчетная схема правила включений-исключений для двух множеств

В случае количества множеств s > 2 процесс нахождения количества элементов объединения A₁ È A₂ È … È A_s заключается в начальном суммировании чисел всех элементов, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Данный процесс дал название формулы.

Пример 1.На выставке представлено 23 картины, в которых использованы только красный и синий цвета. Из них 8 выполнены только в красном цвете, на 11 одновременно использован и красный и синий цвет. Сколько выставлено картин, в которых использован синий цвет?

Решение. Обозначим множество картин, в которых использован красный цвет (только красный и вместе с синим), через A, а множество картин, в которых есть синий цвет, через В. В условии задано общее число картин: N(A È B) = 23, число картин в разности N(A\B) = 8 и число картин в пересечении N(A Ç B) = 11. Подставляя данные значения в формулу для N(A È B), выраженную через разности множеств, получим вначале число картин, в которых использован только синий цвет:

N(B\A) = N(A È B) – N(A\B) – N(A Ç B) = 23–8–11=4.

Искомое общее число картин, в которых использован синий цвет, равно:

N(B) = N(B\A) + N(A Ç B) = 4+11=15.

Ответ: 15.