Элементы теории погрешностей измерений

Положения и выводы физики непосредственно связаны с экспериментом. Как в любой точной науке, в физике результаты экспериментов представляются чаще всего набором некоторых чисел – числовых значений физических величин. Это те самые числовые значения, которые входят в математические формулы, устанавливающие связи между физическими величинами в явлениях природы.

Одна из целей практикума – научиться правильно измерять физические величины и правильно использовать их числовые значения в формулах.

Измерить физическую величину – значит сравнить её с однородной величиной, принимаемой за единичную. Единицы измерения выбирают произвольно, но уж если они выбраны, то должны оставаться неизменными в пределах выбранной системы единиц.

Результатом измерения является числовое значение физической величины; формула А=хВ устанавливает связь измеряемой величины А, её числового значения х и единицы измерения В. Принято различать измерения:

1) прямые, когда измеряется сама исследуемая физическая величина. Сюда относятся измерения с помощью приборов или при непосредственном сравнении с единицей измерения;

2) косвенные, когда искомые значения величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Почему при измерениях возникает необходимость обработки результатов измерений? Потому что произвести измерение абсолютно точно невозможно – всякое измерение сопровождается погрешностью, вызванной принципиальной невозможностью (в силу всеобщей связи явлений в природе) устранить все посторонние влияния на процесс измерения (хотя любое из влияний можно сделать сколь угодно малым).

Если измерительный инструмент обладает достаточной чувствительностью, результаты измерений некоторой величины Х в большинстве случаев различны между собой. Обозначим результаты измерения х₁, х₂, …,х_n, а истинное значение измеряемой величины – х₀, где разности х_i – x₀ = Δx_i – являются погрешностями измерений.

Таким образом, мы оказываемся не в состоянии определить истинное значение измеряемой величины даже в результате большого числа измерений, но мы можем дать истинному значению оценку, т.е. указать его наиболее вероятное значение и указать погрешность измерений. Указание погрешности позволяет вычислить вероятность того, что истинное значение измеряемой величины окажется в том или ином интервале значений.

Принято различать три вида погрешностей: промахи, систематические и случайные погрешности измерения.

Промахи (просчеты) являются результатом низкой квалификации экспериментатора, выполнявшего измерения. Промахи не подаются учету.

Систематические погрешности являются следствием несовершенства приборов, а также недостатков методики измерения. Они всегда дают отклонение результата измерения от истинного значения в одну и ту же сторону. Преодолеваются систематические погрешности путем проверки приборов, более полной разработки теории методики эксперимента и сравнения различных методов измерения одной и той же величины.

Когда говорят об инструментальных погрешностях, то подразумевают погрешности, зависящие от погрешностей применяемых средств измерений. Последние в свою очередь характеризуются классом точности прибора.

Класс точности определяется максимальной погрешностью прибора, выраженной в процентах от полной величины шкалы. Например, класс точности 0,5 означает погрешности в 0,5 % при отклонении стрелки на всю шкалу. При отклонении стрелки на половину шкалы погрешность возрастает в два раза, при отклонении на треть шкалы – в три раза и т.д. Поэтому при измерении с меньшей погрешностью надо выбирать прибор такой чувствительности, чтобы измеряемая величина вызывала отклонение стрелки прибора более чем на половину шкалы.

Величина инструментальной погрешности гарантируется сравнением показаний данного и эталонного приборов. Надежность показаний эталонного прибора рассчитывается с учетом случайных погрешностей.

Случайные погрешности являются следствием случайных, неконтролируемых помех, влияние которых на процесс измерения невозможно учесть непосредственно. Этих помех очень много, они различной физической природы и отличаются силой воздействия на процесс измерения. Можно принимать меры к устранению наиболее влиятельных помех, но все полностью их устранить нельзя. Случайные погрешности могут отклонять результаты измерения от истинного значения в обе стороны и их влияние учитывается посредством определенной обработки результатов измерения физической величины.

Теория погрешностей учитывает только случайные погрешности. Согласно этой теории, случайные погрешности измерений подчиняются закону нормального распределения (закону Гаусса).

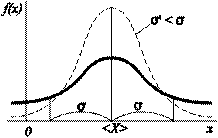
Смысл этого закона заключается в следующем. Допустим, мы хотим измерить некоторую физическую величину, истинное (и нам неизвестное) значение которой есть x₀. Используя какой-нибудь прибор, мы n раз пытаемся определить эту величину, но из–за случайных погрешностей, возникающих в процессе измерения, вместо x₀ получаем набор значений х₁, х₂, …, х_i, …, x_n. Оказывается, с помощью закона распределения мы хотя и не можем указать точно, чему равно х₀, но можем найти с какой вероятностью Р величина x₀ окажется в любом интервале значений а<х₀<b (область значений а<х₀<b называют доверительным интервалом). По закону Гаусса эта вероятность определяется функцией плотности распределения

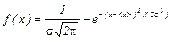(1)

и равна

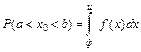. (2)

Здесь х – набор значений, которые мы получаем в результате измерения, <x> – их среднее арифметическое, а σ – среднее квадратическое отклонение:

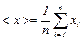, (3)

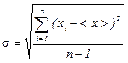. (4)

Как видно из рисунка, гауссова кривая, имеющая на графике симметричный колоколообразный вид, характеризуется двумя параметрами: положением вершины – <x₀> и «шириной» (2σ – расстояние между точками перегиба). Значение <x> обычно и принимают за ту величину, которую надо было измерить, а σ характеризует степень влияния случайных погрешностей на результаты измерения: чем меньше σ, тем уже гауссова кривая и тем, следовательно, точнее проведено измерение.

Обработка результатов серии измерений сводится к возможно более точному нахождению параметров гауссовой кривой <x> и σ. Может показаться, что если произвести большое число измерений (большая серия), то эти параметры можно определить со сколь угодно высокой точностью и, стало быть, можно в пределах одной методики измерений (даже грубой) получить сколь угодно близкое к истинному численное значение измеряемой величины. Однако это не так. Следует еще раз подчеркнуть, что <x> – не истинное значение измеряемой величины, а лишь некоторое приближение к нему.

Чем более широким выбирается доверительный интервал, тем выше вероятность попадания истинного значения измеряемой величины в этот интервал. Мера σ приближения измеренного значения величины <x> к истинному х₀ определяется физической сущностью измеряемой величины, а также физическими и конструктивными принципами, заложенными в методику измерений. Эти принципы в данной методике не зависят от экспериментатора, следовательно, бесконечное увеличение числа измерений не дает заметного увеличения точности.

Поскольку нет смысла стремиться к очень большому числу измерений, то возникает вопрос: как изменится достоверность в зависимости от числа измерений? Зависимость эта сложна и не выражается в элементарных функциях. Существуют специальные таблицы (таблицы коэффициентов Стьюдента), по которым можно определить, во сколько раз надо увеличить стандартный доверительный интервал [±S_x], чтобы при определенном числе измерений n получить требуемую надежность α. За стандартный принимается доверительный интервал [±S_x], где

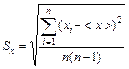. (5)

Здесь х_i– числовое значение величины, полученное при i–м измерении, <x>– среднее арифметическое значение измеряемой величины (3).

Порядок обработки результатов измерений должен быть следующим: выполнив n измерений и записав их результаты в таблицу, вычисляют по (3) среднее арифметическое значение измеряемой величины <x>. Затем по формуле (5) вычисляют стандартный доверительный интервал [±S_x] и находят по таблице коэффициентов Стьюдента t(α,n) в зависимости от требуемой надежности α и числа измерений n. Результат записывают в виде:

х = <x> ± t(α n) S_x,

что означает, что истинное значение измеряемой величины х₀ находится в интервале [<x> – t(α, n) S_x; <x> + t(α, n) S_x] с надежностью (вероятностью) α.

Мерой точности результатов измерений является относительная погрешность, выраженная в процентах:

.

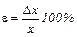Обратная ее величина ψ = 1/ε называется точностью.

Точность результатов обработки должна согласовываться с точностью самих измерений. Вычисления, произведенные с большим, чем необходимо, числом десятичных знаков, требуют лишней затраты сил. Надо придерживаться правила: ошибка вычислений должна быть на порядок меньше ошибки измерения.

Приведенная методика обработки результатов измерений, когда числовое значение измеряемой величины находится по формуле, связывающей ее с величинами, найденными из прямых измерений, ошибка косвенного измерения находится через ошибки прямых измерений по правилу дифференцирования:

.

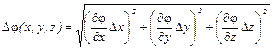На практике при вычислении погрешностей косвенных измерений удобнее сразу вычислять относительную погрешность по правилу дифференцирования натурального логарифма функции. Например,

.

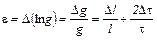Погрешности независимых измерений считаются грубыми или несущественными в зависимости от того, вносят или не вносят они заметный вклад в погрешность окончательного результата. Несущественные погрешности достаточно оценивать приближенно, но обязательно с завышением.