Сочетания. 6.4.1.Сочетания.Любое подмножество из r элементов множества,содержащего k элементов называется сочетанием из k элементов по r.

6.4.1.Сочетания.Любое подмножество из r элементов множества,содержащего k элементов называется сочетанием 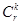из k элементов по r.

Примечания.Если объединить все размещения 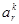из k элементов по r,состоящие из одних и тех же элементов (не учитывая расположения),в классы эквивалентности,то каждому классу будет соответствовать ровно одно сочетание 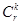и наоборот.

Примеры.1)Пары 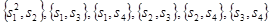исчерпывают все сочетания из четырех элементов по два.

2)Имеется одно сочетание из элементов по 0(т.е.не содержащее ни одного элемента)-это пустое множество.

Число 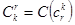всех различных сочетаний равно

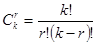
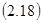
Пример.В числовом лото надо выбрать 5 чисел из 90.Для этого существует способов.

6.4.2. Сочетания с повторениями.Объединим все размещения 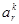с повторением из k элементов по r ,состоящие из одинакового количества одних и тех же элементов (без учета расположения),в классы эквивалентности.Каждый класс эквивалентности называется сочетанием с повторением 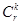из k элементов п о r.

Примечание.Два размещения 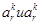или 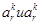принадлежат одному сочетанию 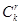или 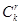соответственно только тогда когда существует перестановка 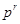множества 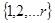такая что для всех имеет место равенство 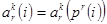или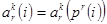

Ср.примечания в 2.2.5.1,2.2.5.2.и2.2.6.1

Число 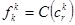различных сочетаний с повторением из элементов по r равно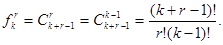

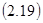
Пример.При наличии двух неразлечимых кубиков можно получить 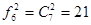различный результат бросаний (ср.пример 7 п.2.2.3.).