Подстановки.

Постановка задач комбинаторики.

Во многих математических исследованиях встречаются комбинаторные задачи, своеобразие которых целесообразно показать на примерах.

1. Скольким способами можно расставить на полке 10 различных книг?

2. как велико число различных отображений, переводящих множество из n элементов в себя?

3. Сколько различных шестизначных чисел можно составить из цифр 1,1,1,5,5,9?

4. В турнире принимают участие восемь команд. Сколько различных предсказаний относительно распределения трех первых мест (по результатам соревнований) можно сделать?

5. Сколько различных трехбуквенных слов можно составить из 32 букв алфавита, не обращая внимание на то, имеют ли смысл составленные из букв слова или нет?

6. Сколькими способами можно из множества k (различных) элементов выбрать r элементов?

7. Как велико число различных результатов бросаний двух не отличимых друг от друга кубиков?

Приведенные примеры показывают, что в задачах комбинаторики интересуются вообще числом различных выборок определенных объектов, причем в зависимости от вида дополнительных требований следует различать, какие выборки считаются одинаковыми и какие различными.

Подстановки.

6.2.1. Подстановки.Каждая последовательность k различных предметов с учетом порядка называется перестановкой этих предметов. Если пронумеровать места этих предметов слева направо: 1,2,…, k, то можно сформулировать следующее определение:

взаимно однозначное отображение p^k конечного упорядоченного множества М = {s₁, s₂ ,…,s_k } из k элементов на себя называется подстановкой элементов множества М.

Перестановки из k элементов множества М отличаются друг от друга только порядком входящих в них элементов.

Число P_k = P(p^k) всех перестановок p^k из k различных элементов равно

P_k = k! (2.10)

Примеры. Для примеров 1 и 2 п. 2.2.3. из (2.10) следует: имеется 10! = 3628800 различных способов расстановки на полке 10 книг из n! Взаимно однозначных отображений, переводящих множество из n элементов в себя.

6.2.2. Группа подстановок k элементов.Если выбрать М ={1,2,…, k,}, то каждую подстановку p^k этих элементов можно записать как матрицу из двух строк:

p^k = ,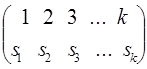

где

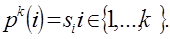
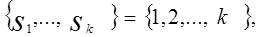
Это делает возможным определение произведение 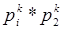двух подстановок k элементов как последовательного проведения обоих преобразований:

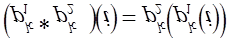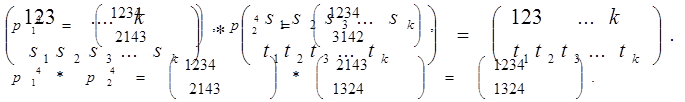
Для этого записывают обе подстановки в виде матриц и переставляют столбцы второго множителя так, чтобы первая строка второго множителя совпадала со второй строкой первого множителя . Матрица произведения состоит из первой строки первого множителя и преобразованной второй строки второго множителя:

Пример1.

Справедливы следующие утверждения .

1)Для каждых двух подстановок 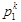и

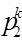
1)Для каждых двух подстановок 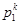и 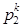элементов множества{1,2,…k} произведение есть 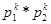однозначно определенная подстановка .

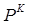2)Произведение есть ассоциативная (но не коммутативная)бинарная операция: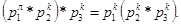

3)Для подстановки 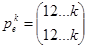(тождественная подстановка) при всех

p^к имеет место равенство .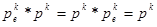

4)Для каждой подстановки 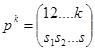существует обратная подстановка 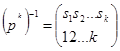для которой выполняется соотношение

(p^k)^-1*p^k=p^k*(p^k)^-1=p^k_e

Вследствие 1)-4) и (2.10)все подстановки р^к элементов множества {1,2…k}образуют {см.2.4.1.6.}группу порядка k!

Эта группа называется симметричной группой S_k.

Пример2.Элементы симметричной группы S_k..

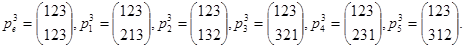
Если в матрице подстановки р^к элементов множества {1,2,…ķ} встречаются два столбца 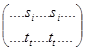для которых s_i<s_j,а t_i>tj(или si>s_j,а t_j<t_i),то талая пара столбцов называется инверсией подстановки р^к.

Подстановка называется четной или нечетной в зависимости от того,четно или нечетно число встречающихся в ней инверсий .

Пример3.Если Z( 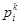)-число иверсий ,то для подстновок примера 2 :

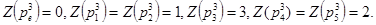
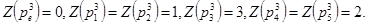
Отображение группы S_k во множество {-1,1},определенное следующим образом: X(p^k)=1,если p^k-четная подстановка,и X(p^k)= -1,если р^к –нечетная подстановка,называется характеристикой подстановки группы S_k..Вследствие равенста X 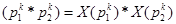это отображение гомоморфно.

Множество всех четных подстановок множества {1,…,k}образуют подгруппу группы S_k порядка k!/2 Эта подгруппа назыается знакопеременной группой.