Размещения. 6.3.1. Размещения. Любой упорядоченный набор r различных элементов множества М, состоящего из k элементов

6.3.1. Размещения. Любой упорядоченный набор r различных элементов множества М, состоящего из k элементов, называется размещением 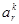из k элементов по r.

Примечание. Каждое размещение 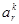есть взаимно однозначное отображение упорядоченного множества {1,2,...,r} во множестве М. из определения следует, что r 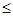k. При r=k получаем подстановки множества М.

Число 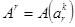различных размещений есть

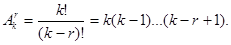
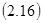
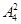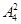Примеры. 1) Имеется различных взаимно однозначных отображений множества {1,2} во множество { }, т.е. = 12.

2) Имеется 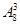= 336 различных способов распределения трех первых мест при восьми командах, участвующих в соревнованиях (ср. пример 4 п. 2.2.3.).

6.3.2. Размещения с повторениями. Любой упорядоченный набор r элементов множества М, содержащего k элементов, называется размещением с повторениями 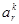из k элементов по r.

Примечание. Каждое размещение с повторением 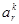есть однозначное отображение упорядоченного множества {1,2,...,r} в М. При этом возможно, что r>k.

Число А( 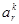) различных размещений с повторениями есть

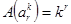
Пример.Число различных трехбуквенных слов, которые можно составить из 32 букв алфавита, есть А( 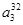)= =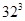32768 (ср. пример 5 п. 2.2.3.)