Подстановка с неподвижной точкой
Если рк-подстановка множества M={1,…,k},то каждый элемент iÎM, для которого pk(i)=i,называется неподвижной точкой подстановки pk.
Пример.Для подстановок примера 2 и 2.2.4.2 справедливо следующее: 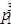

имеет неподвижную 3, 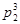 -точку 1,
-точку 1, 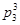 -точку 2,
-точку 2,  имеет неподвижные точки 1,2 и 3;
имеет неподвижные точки 1,2 и 3; 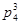 и
и  таковых не имеют.
таковых не имеют.
Число F(p) всех подстановок множества {1,...,k}, имеющих по крайней мере одну неподвижную точку, равно
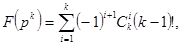
где 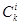 - биномиальные коэффициенты. Число G(
- биномиальные коэффициенты. Число G( 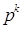 ) всех подстановок множества {1,...,k}, имеющих в точности одну неподвижную точку, равно
) всех подстановок множества {1,...,k}, имеющих в точности одну неподвижную точку, равно 
Пример. Пять человек занимают места за столом, не обращая внимания на разложенные на столе именные карточки. В общей сложности они могут разместиться 5! = 120 способами. В
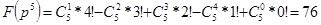
случаях по крайней мере один человек и в
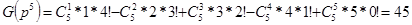
случаях по крайней мере один человек займет отведенное ему место.
6.2.4. Подстановки с заданным числом циклов. Если матрицу подстановки p перестановкой столбцов можно привести к виду
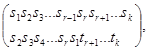
то  задает взаимно однозначное отображение ,
задает взаимно однозначное отображение , 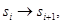 i=1,2,...,r-1,
i=1,2,...,r-1, 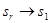 , множества
, множества 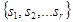 на себя, которое называется циклом длины r и обозначается
на себя, которое называется циклом длины r и обозначается 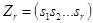 . В соответствии с этим каждой неподвижной точке соответствует цикл длины 1.
. В соответствии с этим каждой неподвижной точке соответствует цикл длины 1.
Каждую подстановку 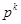 можно однозначно (с точностью до порядка сомножителей) представить в виде произведения циклов, не имеющих общих элементов.
можно однозначно (с точностью до порядка сомножителей) представить в виде произведения циклов, не имеющих общих элементов.
Примеры.
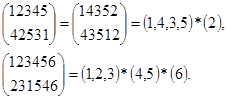
Для числа P(k,s) подстановок 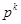 , которые могут быть представлены в виде произведения s циклов, имеют место рекуррентные формулы
, которые могут быть представлены в виде произведения s циклов, имеют место рекуррентные формулы
P(k,k) = 1, P(k,1) = (k-1)! при k 1, (2.14)
P(k,s) = P(k-1,s-1)+(k-1)*P(k-1,s) при k>s 2.
Пример. Имеется P(3,3)=1 подстановка группы 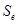 (ср. пример 2 и 2.2.4.2) с тремя циклами:
(ср. пример 2 и 2.2.4.2) с тремя циклами: 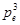 ; P(3,1) = 2 подстановки с одним циклом:
; P(3,1) = 2 подстановки с одним циклом:  ; P(3,2) = P(2,1) + 2*P(2,2) = 1+2*1 с двумя циклами:
; P(3,2) = P(2,1) + 2*P(2,2) = 1+2*1 с двумя циклами: 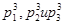 .
.
6.2.5.Перестановкис повторениями. Если рассматривать упорядоченные k-наборы из множества М, то получим перестановки с повторениями.
Пусть М = { 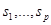 } - непустое множество из р элементов и
} - непустое множество из р элементов и  -натуральные числа такие, что
-натуральные числа такие, что  Каждый упорядоченный набор k чисел
Каждый упорядоченный набор k чисел  , содержащий элемент
, содержащий элемент 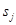 ровно
ровно 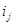 раз ( 1<j<p), называется перестановкой множества М с повторением.
раз ( 1<j<p), называется перестановкой множества М с повторением.
Примечание. При i=i=...=i=1 получим перестановку множества из р элементов.
Число 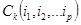 различных перестановок множества М с повторениями равно *).
различных перестановок множества М с повторениями равно *).
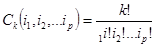
где 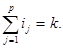
Пример. Имеется 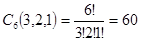 различных шестизначных чисел, содержащих трижды цифру 1, дважды цифру 5 и один раз цифру 9 (ср. пример 3 и 2.2.3.).
различных шестизначных чисел, содержащих трижды цифру 1, дважды цифру 5 и один раз цифру 9 (ср. пример 3 и 2.2.3.).
Дата добавления: 2015-10-05; просмотров: 1102;
